Kuliah Asinkron Matematika 2
Summary
TLDRThis tutorial video focuses on teaching calculus, specifically integrals, to students. The instructor begins by offering a prayer and explaining the importance of practicing different types of integrals, including definite and indefinite integrals, as well as double and triple integrals. Throughout the session, the instructor demonstrates various examples, such as integrals of polynomials and trigonometric functions, offering clear step-by-step solutions. Students are encouraged to follow along, check their answers, and upload their work as proof of participation. The video serves as a helpful review for final assessments and aims to reinforce integral concepts through detailed examples.
Takeaways
- 😀 The tutorial begins with a prayer for knowledge and ease of understanding for all participants.
- 😀 The session covers two main topics: definite and indefinite integrals (CPMK 1), and double and triple integrals (CPMK 2).
- 😀 The first example demonstrates solving an indefinite integral, highlighting the steps for finding the integral of 2x^3 + 2x^2 - x + 5 dx.
- 😀 The second example explains solving a definite integral, using the integral from 1 to 3 of the function x^2 - 2x + 1 dx.
- 😀 The third example introduces the concept of substitution in integrals, using u = 3x + 2, to simplify the integral of 2cos(3x + 2) dx.
- 😀 For CPMK 2, the focus shifts to double integrals, with an example showing how to solve the integral of x^2 dx from 0 to 1.
- 😀 The process of solving double integrals is explained step by step, using the concept of integrating from the outer variable to the inner variable.
- 😀 The tutorial also introduces triple integrals, with an example showing the integration process for the expression 1 - 2z + 1 dz.
- 😀 In the triple integral example, the steps include integrating with respect to z, followed by x, and finally y, using appropriate limits for each variable.
- 😀 The tutorial concludes with a reminder to check for any mistakes in the calculations and to upload the completed work as proof of participation.
Q & A
What is the first topic covered in the tutorial?
-The first topic covered in the tutorial is about integrals, both definite and indefinite.
What is the first example problem presented in the tutorial?
-The first example problem involves the indefinite integral of the function 2x^3 + 2x^2 - x + 5, with respect to x.
What is the general solution for the first integral problem?
-The solution for the first integral problem is 1/2x^4 - 1/2x^2 + 5x + C.
How does the second integral problem differ from the first?
-The second problem is a definite integral, as it involves specific upper and lower bounds (from x = 1 to x = 3).
What method is used to solve the second integral problem?
-The second integral is solved using the fundamental theorem of calculus, applying the limits of integration (x = 3 and x = 1) to the antiderivative.
What is the result of the second integral problem?
-The result of the second integral problem is 2.66 after evaluating the definite integral.
What substitution is used in the third integral problem?
-In the third integral problem, a substitution method is used where u = 3x + 2, which simplifies the integral.
What is the result of the third integral after substitution?
-The result of the third integral is (2/3) sin(3x + 2) + C.
What is the focus of CPMK2 in the tutorial?
-CPMK2 focuses on double and triple integrals, including examples with two variables and three variables.
What is the first example problem in CPMK2?
-The first example in CPMK2 involves a double integral of the function x^2, with respect to x, integrated from 0 to 1.
How does the solution for the double integral problem proceed?
-The solution proceeds by first evaluating the inner integral, followed by evaluating the outer integral to get a final result of 1/3.
What is the approach for solving the triple integral problem?
-In the triple integral problem, the integration is performed step by step, starting from the innermost variable and moving outwards.
What is the result of the triple integral example?
-The result of the triple integral example is 9, after evaluating the integral with the specified limits.
What does the final integral problem involve?
-The final problem involves a double integral in the form of 10 * 2x * yz, with respect to z and x.
What is the outcome of the final integral problem?
-The outcome of the final integral problem is -3/2y, after performing the integration with respect to both variables.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
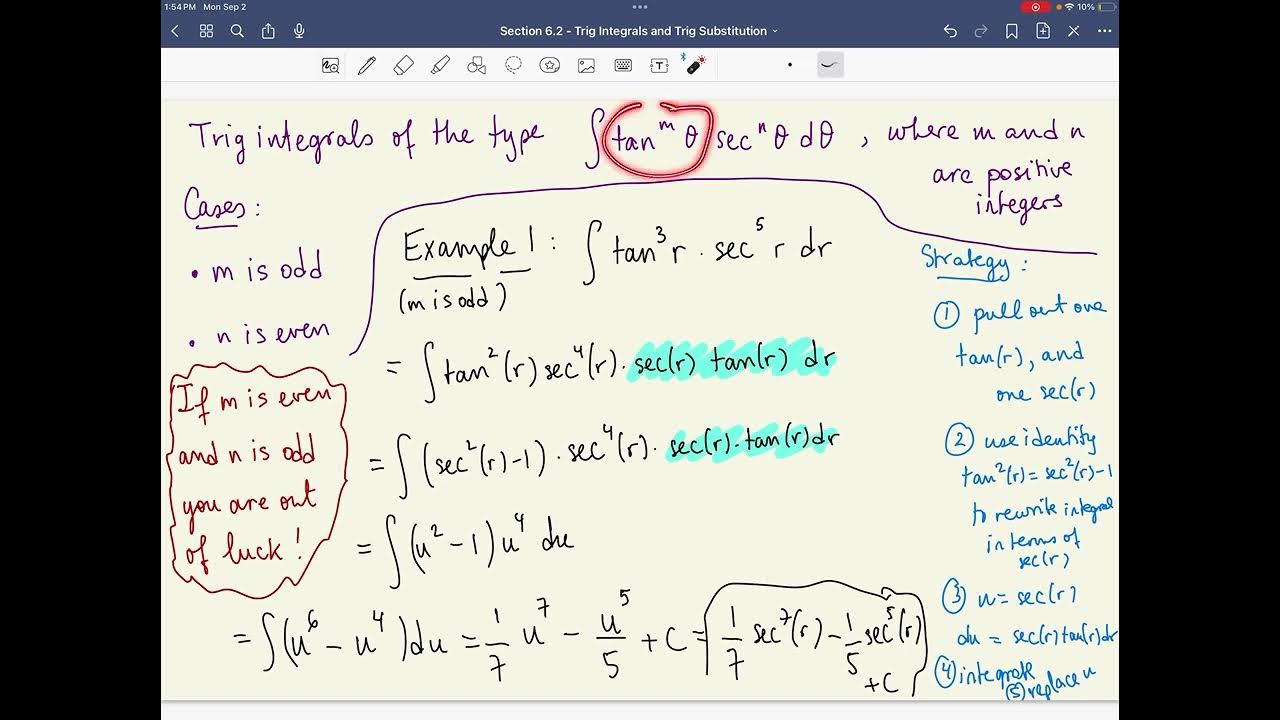
Section 6.2 - Trig integrals and substitution - Part 2

Eps.2 KALKULUS 2: Teknik Integrasi - Teknik Substitusi

Integral Trigonometri Dasar, Substitusi & Menggunakan Identitas Trigonometri (Integral Part 6)

Konsep Dasar Integral Fungsi Aljabar (Integral Part 1) M4THLAB

KALKULUS INTEGRAL - INTEGRAL TAK WAJAR

✅INTEGRALES trigonométricas con POTENCIAS [𝙚𝙣 4 𝙋𝙖𝙨𝙤𝙨 😎🫵💯 ] Cálculo Integral
5.0 / 5 (0 votes)
