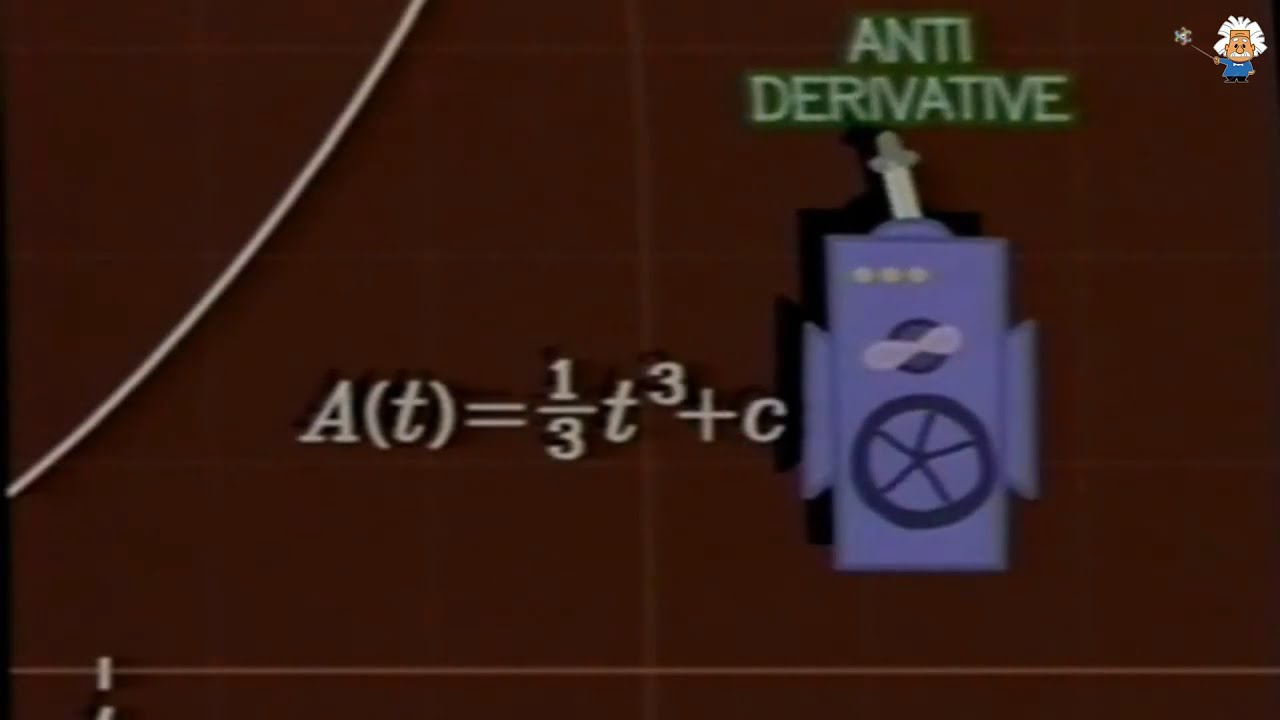07 - Integração.

Summary

This video script delves into the development of calculus, tracing its evolution from ancient Greece to the groundbreaking discoveries of Isaac Newton and Gottfried Wilhelm Leibniz in the 17th century. It highlights their respective contributions to the field, touching upon key concepts such as integration, differentiation, and their profound impact on mathematics and science. The narrative explores the rivalry between Newton and Leibniz over the invention of calculus, their contrasting approaches, and how their work ultimately transformed the way we understand motion, acceleration, and areas under curves, shaping modern scientific thought.

Takeaways

• 😀 The method for calculating the area of curved figures, known as integration, was fully developed in the 17th century, marking a significant breakthrough in mathematics.
• 😀 Isaac Newton, born in the same year as Galileo's death, was a key figure in the development of calculus, though his discoveries were not solely his own.
• 😀 Newton's early life was marked by an unusual brilliance, despite coming from a family with limited resources. His mother recognized his potential and sent him to university.
• 😀 Newton and Leibniz, two major figures in the development of calculus, had distinct personalities and approaches, but both contributed immensely to mathematics.
• 😀 Newton’s calculus was based on the method of fluxions, and while it was a major step forward, the process of discovering calculus was deeply influenced by earlier work, including that of Galileo and Archimedes.
• 😀 Archimedes, using geometry, nearly discovered the principles of calculus centuries before, with notable work like the quadrature of a parabola.
• 😀 The Greeks pioneered early methods like the method of exhaustion to approximate areas under curves, an early form of integration that laid the groundwork for later developments.
• 😀 Galileo, Kepler, and other scientists contributed to the understanding of motion, speed, and acceleration, problems that would later be addressed by differential calculus.
• 😀 The connection between differentiation and integration was a crucial discovery, allowing mathematicians to see that these two processes are inversely related, a key component of the Fundamental Theorem of Calculus.
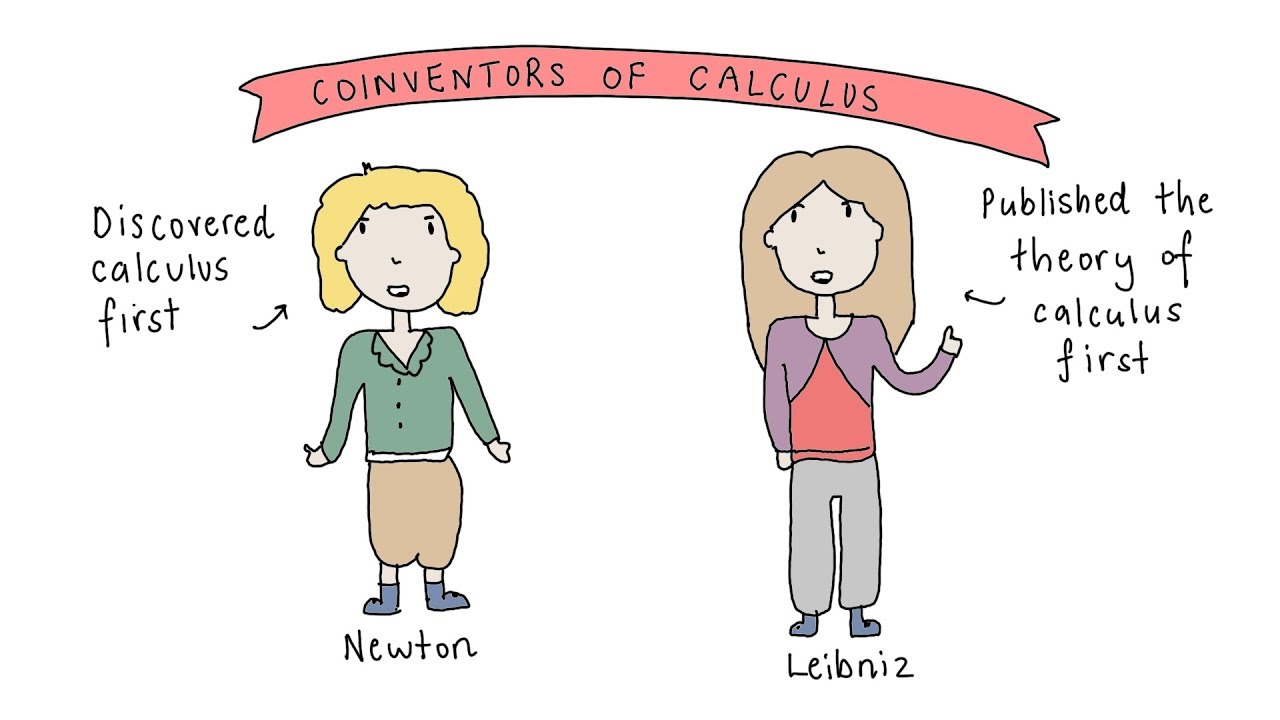
• 😀 Despite their shared contributions, the controversy between Newton and Leibniz over the invention of calculus led to academic disputes that would continue for years, highlighting the competitive nature of scientific discovery.

Q & A

What was the key mathematical breakthrough achieved in the 17th century?

The key breakthrough was the development of the method of integration, which allowed for the calculation of areas of curved figures, and this laid the foundation for the discovery of calculus.

What role did Isaac Newton play in the development of calculus?

Isaac Newton, along with others, made groundbreaking contributions to the development of calculus. He discovered the concept of derivatives and integration, which he later used to explain physical phenomena like the motion of objects.

Who else, besides Newton, contributed to the development of calculus?

Gottfried Wilhelm Leibniz was a key contributor alongside Newton. He independently developed his version of calculus, and his notation for integrals is still used today.

What is the method of exhaustion, and how did it relate to the Greeks?

The method of exhaustion was an ancient Greek technique to approximate the area of curved figures by inscribing polygons with increasingly more sides. It is a precursor to integral calculus and was used by mathematicians like Archimedes.

How did the Greeks influence the development of calculus?

The Greeks laid the groundwork by exploring the properties of curves, such as finding areas and volumes of specific shapes, and developing early methods like the method of exhaustion. These ideas were foundational for the later development of calculus.

Why was Newton’s development of calculus significant in science and mathematics?

Newton’s calculus was a powerful tool for solving real-world problems in physics, particularly in understanding motion and the laws of nature, such as gravity. It also provided a mathematical framework for analyzing dynamic systems.

What was the controversy surrounding the invention of calculus?

There was a major dispute between Newton and Leibniz over the priority of their discoveries. Leibniz’s notation for calculus became widely adopted, while Newton's work remained largely unpublished during his lifetime, fueling accusations of plagiarism.

How did the discovery of calculus impact the study of motion?

Calculus allowed scientists to describe motion quantitatively through derivatives (for velocity) and integrals (for displacement). It became essential for understanding acceleration, force, and other dynamic physical properties.

What is the first fundamental theorem of calculus?

The first fundamental theorem of calculus states that integration and differentiation are inverse operations. This means that if you integrate a function and then differentiate the result, you return to the original function, up to a constant.

What did Newton mean by 'standing on the shoulders of giants'?

Newton's famous quote, 'If I have seen further, it is by standing on the shoulders of giants,' refers to his acknowledgment that his discoveries were built upon the work of previous great scientists like Galileo and Kepler.