Understanding the Rotation Matrix
Summary
TLDRIn this video, the concept of 2D rotation matrices is explored, explaining how to construct a matrix to rotate points around the origin by any chosen angle. The video covers essential properties of rotation matrices, including their inverses, determinants, and how combining rotations results in another rotation matrix. The focus shifts to 3D rotations, using the Z-axis as an example and introducing the right-hand rule. For more complex 3D rotations, the video explains the approach of sequential rotations around the primary axes and the difference between intrinsic and extrinsic rotations. The video also touches on Euler angles and their applications in robotics.
Takeaways
- 😀 Rotation matrices are used to rotate points around the origin in 2D and 3D spaces, allowing for transformations in geometric space.
- 😀 The 2D rotation matrix can be derived using trigonometric identities and is given by [ cos(θ) -sin(θ); sin(θ) cos(θ) ], where θ is the angle of rotation.
- 😀 The inverse of a rotation matrix is its transpose, meaning rotating by an angle θ and then by -θ will undo the rotation.
- 😀 The determinant of any rotation matrix is always 1, regardless of the rotation angle.
- 😀 Multiplying two rotation matrices results in another rotation matrix, meaning multiple rotations can be combined into one.
- 😀 Rotation matrices are part of the special orthogonal group (SO2 for 2D and SO3 for 3D), ensuring their key properties are maintained across dimensions.
- 😀 In 3D, rotations around the Z-axis can be described using a 3x3 matrix with a 1 in the bottom right corner, ensuring the Z-coordinate remains unchanged.
- 😀 To rotate a point around a specific axis (X, Y, or Z), the respective rotation matrix is constructed by setting 1's along the diagonal and adjusting the rest with cos(θ) and sin(θ).
- 😀 A 3D rotation can be performed sequentially by combining rotations around different axes (e.g., X, Y, and Z) in a specific order, known as extrinsic rotations.
- 😀 Intrinsic rotations differ in that the rotation axes move with the object, as opposed to extrinsic rotations where the axes remain fixed, leading to different results depending on the order of operations.
Q & A
What is a 2D rotation matrix and how is it derived?
-A 2D rotation matrix is a matrix used to rotate points around the origin by a specified angle. It is derived using trigonometric identities. The matrix for rotating points anticlockwise by an angle θ is given as: [cos(θ), -sin(θ); sin(θ), cos(θ)]. This matrix is derived by using a point's polar coordinates and applying trigonometric expansions.
What are the key properties of rotation matrices?
-Rotation matrices have several key properties: 1. The inverse of a rotation matrix is its transpose. 2. The determinant of a rotation matrix is always 1. 3. Multiplying two rotation matrices results in another rotation matrix. These properties are true for both 2D and 3D rotations.
How does the inverse of a rotation matrix work?
-The inverse of a rotation matrix is simply its transpose. This is because rotating by an angle θ and then by -θ (the inverse) results in no change to the original point, which is equivalent to undoing the rotation. This property is particularly useful in 3D rotations.
What does it mean for rotation matrices to form a group, and what is SO(n)?
-Rotation matrices form a group called the special orthogonal group. SO(n) represents the group of all rotation matrices in n-dimensional space. For example, SO2 refers to rotation matrices in 2D, and SO3 refers to those in 3D. These groups have special properties such as preserving the length of vectors.
What are the challenges of 3D rotations compared to 2D rotations?
-While 2D rotations are relatively simple to understand and calculate, 3D rotations are more complex due to the multiple axes of rotation and the need to account for rotations around different axes. In 3D, rotations are often performed sequentially around the X, Y, and Z axes, and the order of these rotations can lead to different results.
What is the Z-axis rotation in 3D, and how does it differ from 2D rotation?
-In 3D, a rotation around the Z-axis involves rotating a point in the XY-plane while keeping its Z-value constant. The 3x3 rotation matrix for a Z-axis rotation looks similar to the 2x2 matrix for 2D rotation but with an added row and column for the Z-axis. This maintains the Z-coordinate unchanged during the rotation.
What is the right-hand rule for rotations?
-The right-hand rule for rotations states that if you point the thumb of your right hand along the positive axis (X, Y, or Z), your fingers curl in the direction of positive rotation around that axis. This rule is used to determine the direction of rotation and is commonly used in both mathematics and robotics.
How do you perform 3D rotations around the X, Y, or Z axes?
-To perform 3D rotations around the X, Y, or Z axes, you use 3x3 rotation matrices. The matrix for rotation around each axis involves cosine and sine terms, with the axis of rotation remaining unchanged. For example, for rotation around the Z-axis, the matrix has 1 in the Z position and cosine and sine values for the X and Y positions.
What are intrinsic and extrinsic rotations in 3D?
-Intrinsic rotations involve rotating the coordinate system itself, with each successive rotation occurring around the rotated axes. Extrinsic rotations, on the other hand, involve rotating points in the original coordinate system. The order of rotations is different in these two cases, leading to different results.
How can complex 3D rotations be broken down into simpler rotations?
-Complex 3D rotations can be decomposed into a sequence of up to three simpler rotations around the primary axes (X, Y, and Z). The order of rotations is important; for instance, rotating around Z, then Y, then X is different from rotating around X, Y, and Z. The final rotation matrix is obtained by multiplying the individual matrices together, considering the correct order of operations.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Transformasi Geometri Bagian 3 - Rotasi (Putaran) Matematika Wajib Kelas 11
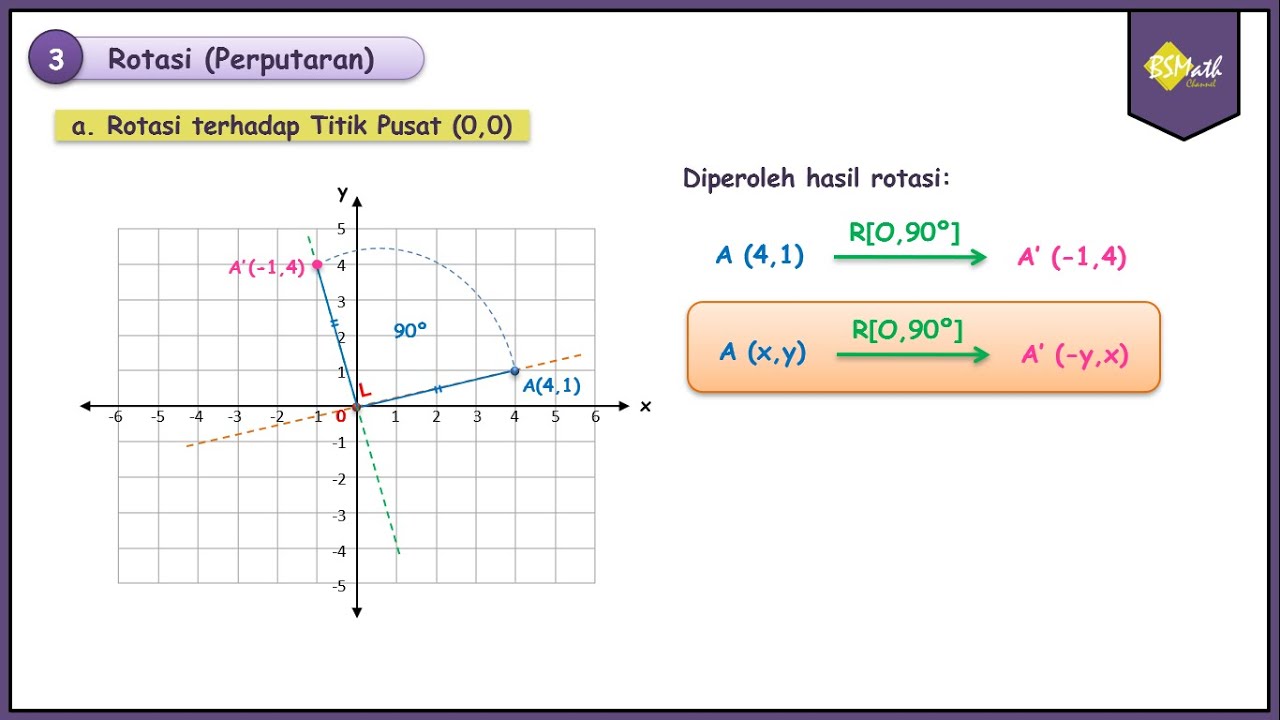
Rotasi Terhadap Titik Pusat O(0,0) - Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka
Rotation Matrix Parametrization

How to make a 3D Renderer [Explained Simply]

Grafika Komputer : Pertemuan 7 (Part 1) Transformasi 2D dengan Metode Konvensional

Rotasi Hal 34-36 Bab 1 TRANSFORMASI FUNGSI Kelas 12 SMA SMK Kurikulum Merdeka
5.0 / 5 (0 votes)
