The Pythagorean Theorem: Extensions and Applications
Summary
TLDRThis video explores various applications of the Pythagorean theorem, starting with finding the distance between points on an XY grid, such as those used in computer graphics. It explains how to calculate this distance using the difference in coordinates and introduces the concept of delta (Δ) for differences. The video then extends the theorem to three dimensions, illustrating how to find distances across 3D objects using a similar approach. Finally, it demonstrates how to derive the equation of a circle on a plane, showing practical uses of the Pythagorean theorem in algebra and geometry.
Takeaways
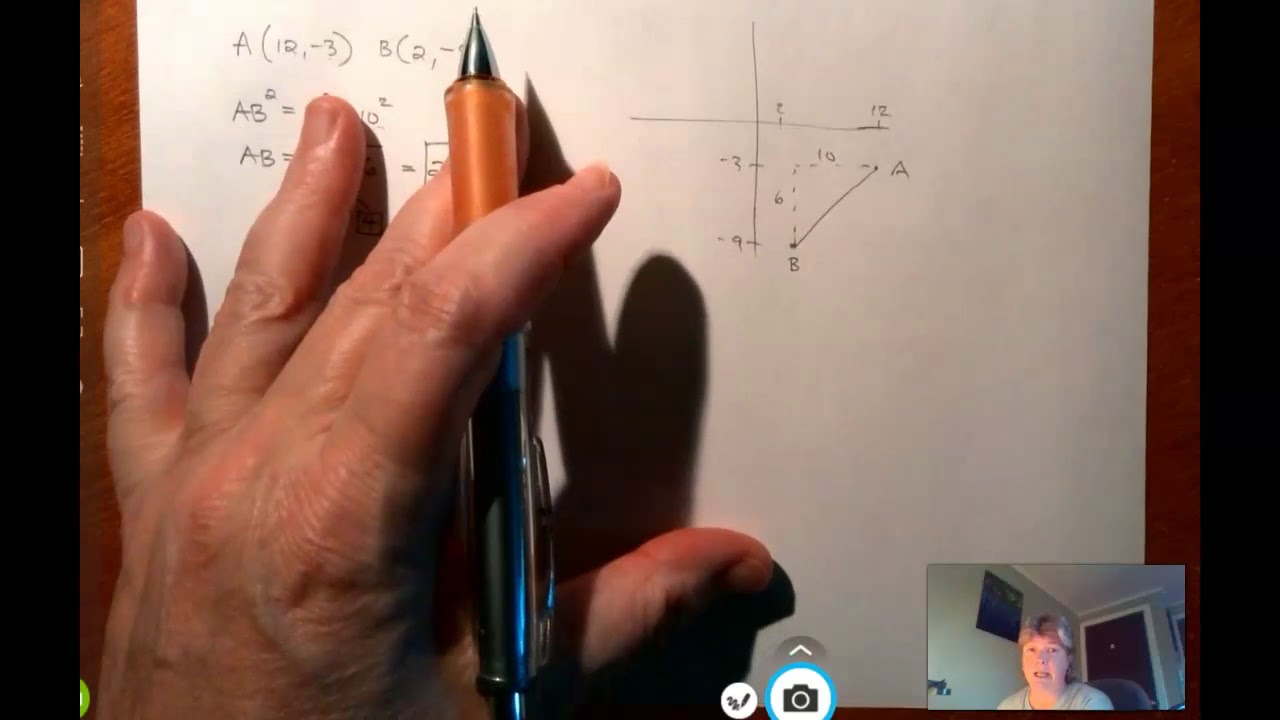
- 📏 The video discusses extensions and applications of the Pythagorean theorem, focusing on finding distances between points on a graph.
- 📉 The distance formula can be applied to find the distance between two points on an XY grid by creating a right triangle and using the Pythagorean theorem.
- 🔢 To find the horizontal and vertical distances between points, subtract the respective X and Y coordinates and use these differences in the distance formula.
- 🔄 The formula for the distance between two points on a plane is derived by squaring the differences in X and Y values, adding them, and taking the square root.
- 🌐 The video extends the concept to three dimensions, explaining how to find the diagonal distance across a three-dimensional object using a similar approach.
- 🏠 In three dimensions, the distance formula incorporates the length, width, and height of the object, leading to a generalized Pythagorean theorem for 3D space.
- 🔍 The process of finding the diagonal in 3D involves first finding the distance across the floor (a 2D problem) and then using this distance in a new right triangle that includes the height.
- 📐 The video also explains how to find the equation of a circle on a plane, using the Pythagorean theorem to relate the radius and the coordinates of points on the circle.
- 🔵 The equation of a circle is derived from the relationship between the radius and the coordinates of any point on the circle, written as x^2 + y^2 = r^2.
- 🎨 Applications in graphics and geometry software are highlighted, showing how programs like GeoGebra use these equations to plot circles and other shapes on a coordinate plane.
Q & A
What is the primary application of the Pythagorean theorem discussed in the video?
-The primary application discussed is finding the distance between two points on an XY grid using the Pythagorean theorem.
How is the distance between two points on a graph calculated?
-The distance is calculated by finding the horizontal and vertical distances between the points, squaring them, adding the squares, and then taking the square root of the sum.
What are Delta X and Delta Y in the context of the distance formula?
-Delta X represents the difference in the X coordinates of the two points, and Delta Y represents the difference in the Y coordinates.
How does the video extend the Pythagorean theorem to three dimensions?
-The video extends the Pythagorean theorem to three dimensions by demonstrating how to calculate the diagonal distance across a three-dimensional object using the lengths, widths, and heights of the sides.
How is the diagonal distance across a three-dimensional space calculated?
-The diagonal distance is calculated by taking the square root of the sum of the squares of the length, width, and height.
What is the equation for a circle derived in the video?
-The equation for a circle is \( x^2 + y^2 = r^2 \), where r is the radius of the circle.
How is the concept of a right triangle used to find the equation of a circle?
-The concept is used by noting that the radius forms the hypotenuse of a right triangle, with the legs being the X and Y coordinates, thus leading to the equation \( r^2 = x^2 + y^2 \).
What is the significance of using coordinate numbers in calculating distances on a graph?
-Using coordinate numbers allows for precise distance calculations, which is crucial when dealing with non-integer or decimal coordinates where simply counting squares is not feasible.
How does the video suggest visualizing three-dimensional space for applying the extended Pythagorean theorem?
-The video suggests visualizing the room you're in as a box-like structure and imagining the diagonal distance between a top corner and an opposite bottom corner.
What practical applications of the distance formula are mentioned in the video?
-Practical applications mentioned include plotting graphics on a computer screen, determining distances in various fields like graphic design, and defining geometrical shapes like circles.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Como calcular la DISTANCIA entre dos puntos en el PLANO CARTESIANO. Usando el Teorema de Pitagoras.

Panjang Vektor | Modulus Vektor dan Vektor Satuan (Vektor Bagian 6) Matematika Peminatan Kelas X

What Are Distance and Displacement? | Physics in Motion

Distancia entre dos puntos
Distance and Midpoint

Soal soal TKA Matematika Jenjang SMP 2026 Materi Geometri dan Pengukuran | Part 3
5.0 / 5 (0 votes)
