Kelas VIII - Apa itu Teorema Pythagoras?
Summary
TLDRThis video explains the concept of the hypotenuse in right triangles and introduces the Pythagorean theorem. It clarifies that the hypotenuse is the longest side of a right triangle, opposite the right angle. The Pythagorean theorem is then explained, stating that the square of the hypotenuse is equal to the sum of the squares of the other two sides. The video further demonstrates how to use the theorem to calculate the sides of a right triangle, both for finding the hypotenuse and the other sides using simple formulas.
Takeaways
- 😀 The term 'sisi miring' refers to the longest side of a right-angled triangle, which is opposite the right angle and is also known as the hypotenuse.
- 😀 In determining the hypotenuse ('sisi miring'), its position is not the key factor; rather, it must be the longest side, opposite the right angle.
- 😀 The concept of the hypotenuse is explained using visual examples to help clarify its location in various triangles.
- 😀 The Pythagorean Theorem states that the square of the hypotenuse equals the sum of the squares of the other two sides: c² = a² + b².
- 😀 The Pythagorean Theorem is applicable to right-angled triangles, and its formula helps to calculate unknown side lengths if the other sides are known.
- 😀 Example: A triangle with sides 3, 4, and 5 demonstrates that 3² + 4² = 5², thus proving the Pythagorean Theorem.
- 😀 The theorem is further illustrated using squares constructed on the sides of the triangle to visually confirm the relationship between the sides.
- 😀 When calculating an unknown side, the Pythagorean Theorem can be rearranged to solve for either a or b: a² = c² - b² or b² = c² - a².
- 😀 To calculate the length of a side in a right triangle, you can use square roots, as in √(c² - b²) to find 'a' or √(c² - a²) to find 'b'.
- 😀 The video concludes with an encouragement to continue studying and understanding the application of the Pythagorean Theorem in geometric problems.
Q & A
What is the definition of the hypotenuse in a right triangle?
-The hypotenuse is the longest side of a right triangle, and it is opposite the right angle.
What are the two conditions that define the hypotenuse?
-The two conditions are: the hypotenuse must be the longest side of the right triangle, and it must be opposite the right angle.
Why is the term 'hypotenuse' used interchangeably with 'side miring'?
-The term 'hypotenuse' refers to the same side as 'side miring', which is the longest side opposite the right angle in a right triangle.
What should we focus on to identify the hypotenuse in a triangle?
-To identify the hypotenuse, look for the longest side that is opposite the right angle in a right triangle.
What is the Pythagorean theorem?
-The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (c²) is equal to the sum of the squares of the two other sides (a² + b²).
What does the equation 'c² = a² + b²' represent?
-The equation 'c² = a² + b²' represents the Pythagorean theorem, where c is the hypotenuse and a and b are the two other sides of a right triangle.
How is the Pythagorean theorem verified using squares?
-The theorem can be verified by calculating the area of squares built on the sides of a right triangle. The sum of the areas of the squares on the two shorter sides (a² + b²) equals the area of the square on the hypotenuse (c²).
How can we use the Pythagorean theorem to find a missing side in a right triangle?
-To find a missing side, rearrange the Pythagorean theorem: For the hypotenuse, use c = √(a² + b²). For the other sides, subtract the square of the known side from the square of the hypotenuse: a = √(c² - b²) or b = √(c² - a²).
If you know the hypotenuse and one side, how can you find the other side?
-If you know the hypotenuse (c) and one side (either a or b), you can find the other side using the formula: a = √(c² - b²) or b = √(c² - a²).
Why is it important to understand the concept of the hypotenuse and Pythagorean theorem?
-Understanding the hypotenuse and the Pythagorean theorem is essential for solving problems involving right triangles, as it allows you to calculate missing sides and verify relationships between the sides of a triangle.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Teorema Pythagoras [Part 1] - Menentukan Panjang Salah Satu Sisi Pada Segitiga Siku-siku
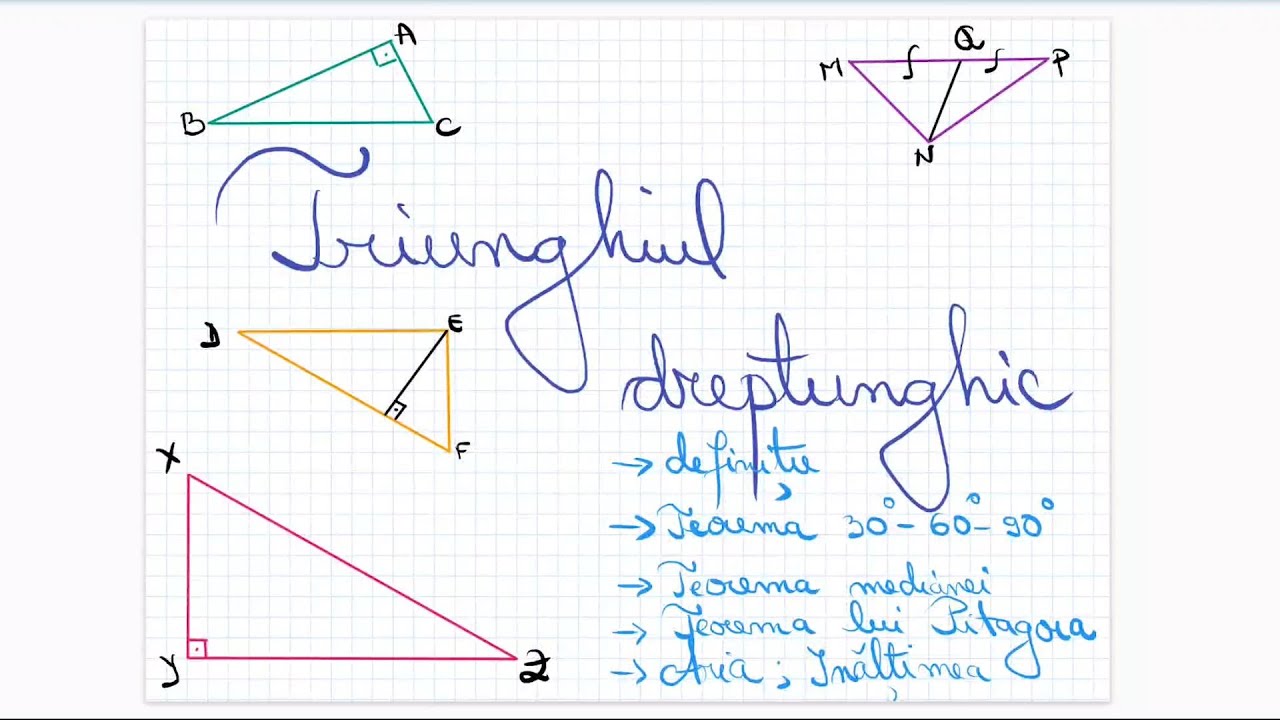
Triunghiul dreptunghic, teorema 30 60 90, teorema medianei, teorema lui Pitagora si reciproca, arie
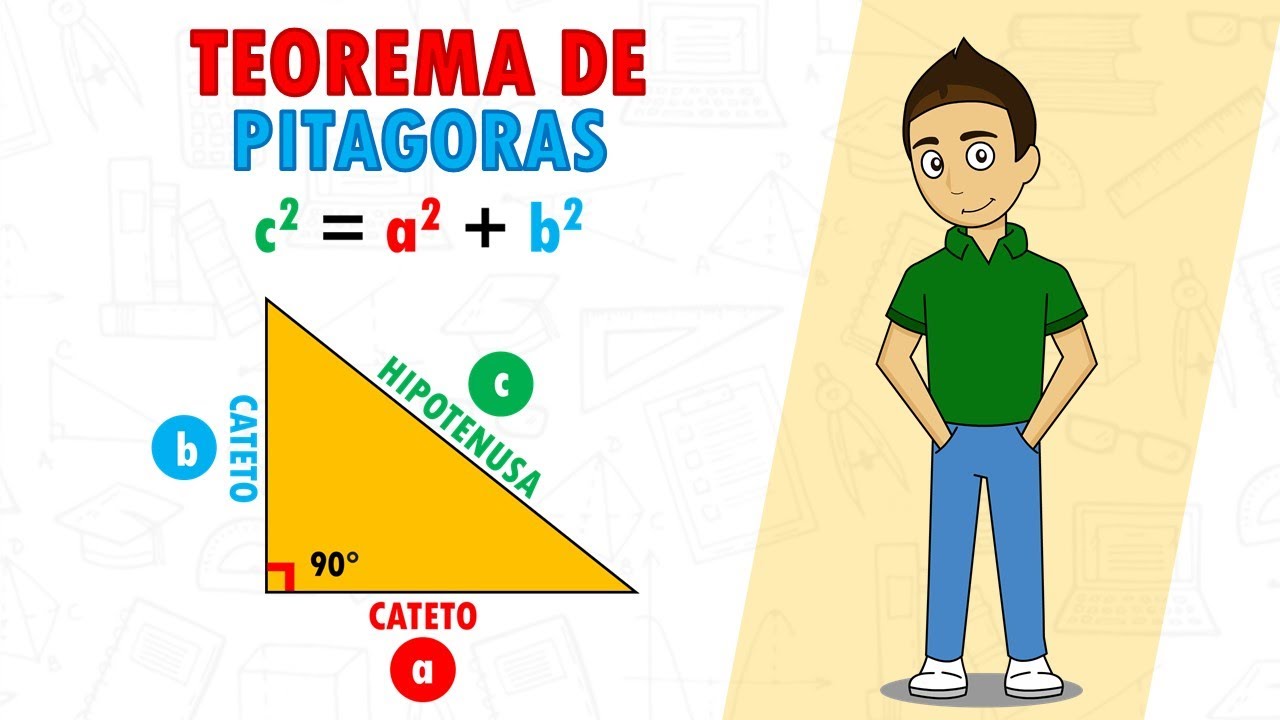
TEOREMA DE PITAGORAS Super Facil - Para principiantes

Kurikulum Merdeka Matematika Kelas 8 Bab 2 Teorema Pythagoras

Introdução ao Teorema de Pitágoras | Geometria | Khan Academy
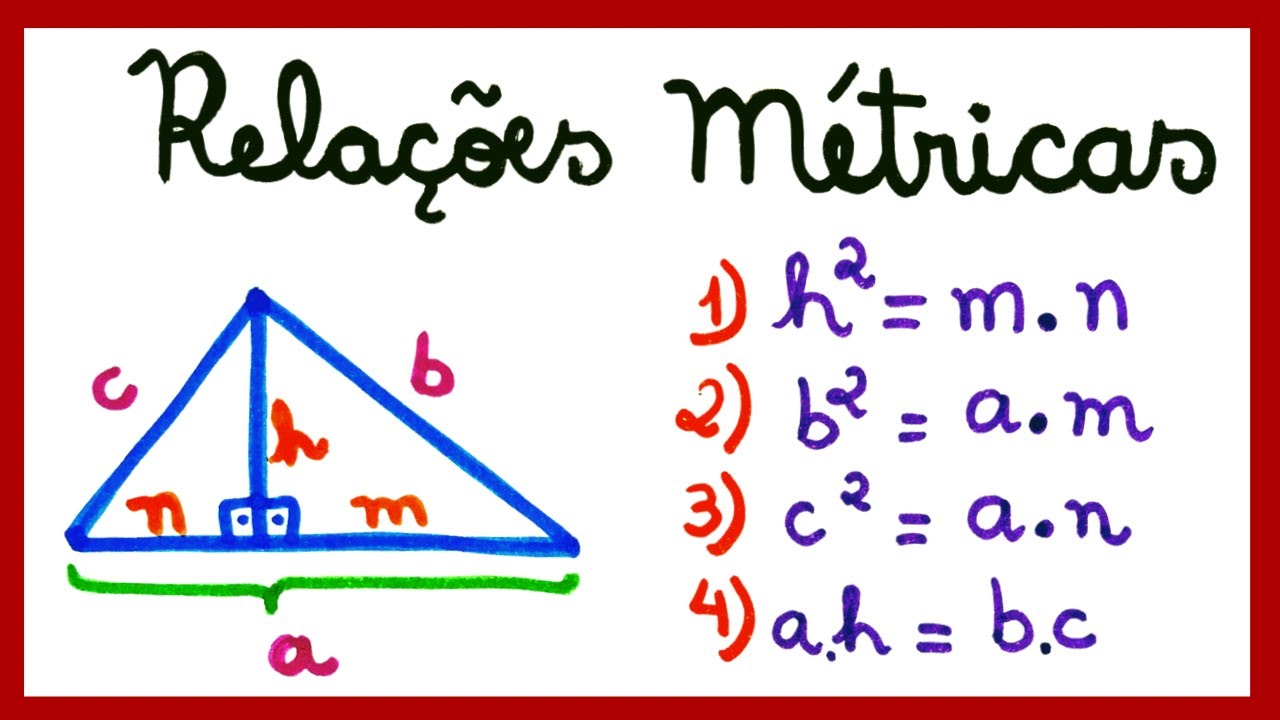
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO!!
5.0 / 5 (0 votes)
