GARIS DAN SUDUT (PART 2)

Summary

In this educational video, the presenter delves into the concepts of angles, focusing on the relationship between lines and angles. Key topics covered include types of angles, such as complementary and supplementary angles, and the various relationships between intersecting and parallel lines. The video provides clear examples of how lines interact geometrically, explaining terms like intersecting, parallel, and skew lines. Additionally, the video includes problem-solving exercises to help viewers apply the concepts. The lesson emphasizes creativity in solving geometry problems and understanding the relationships between angles and lines.

Takeaways

• 😀 The lesson is focused on understanding lines and angles, particularly their relationships in geometry.
• 😀 The concept of different types of lines is introduced, such as intersecting, parallel, and skew lines.
• 😀 Lines can either intersect, be parallel (never meet), or skew (not parallel but do not meet).
• 😀 Coincident lines are lines that overlap exactly, sharing the same space.
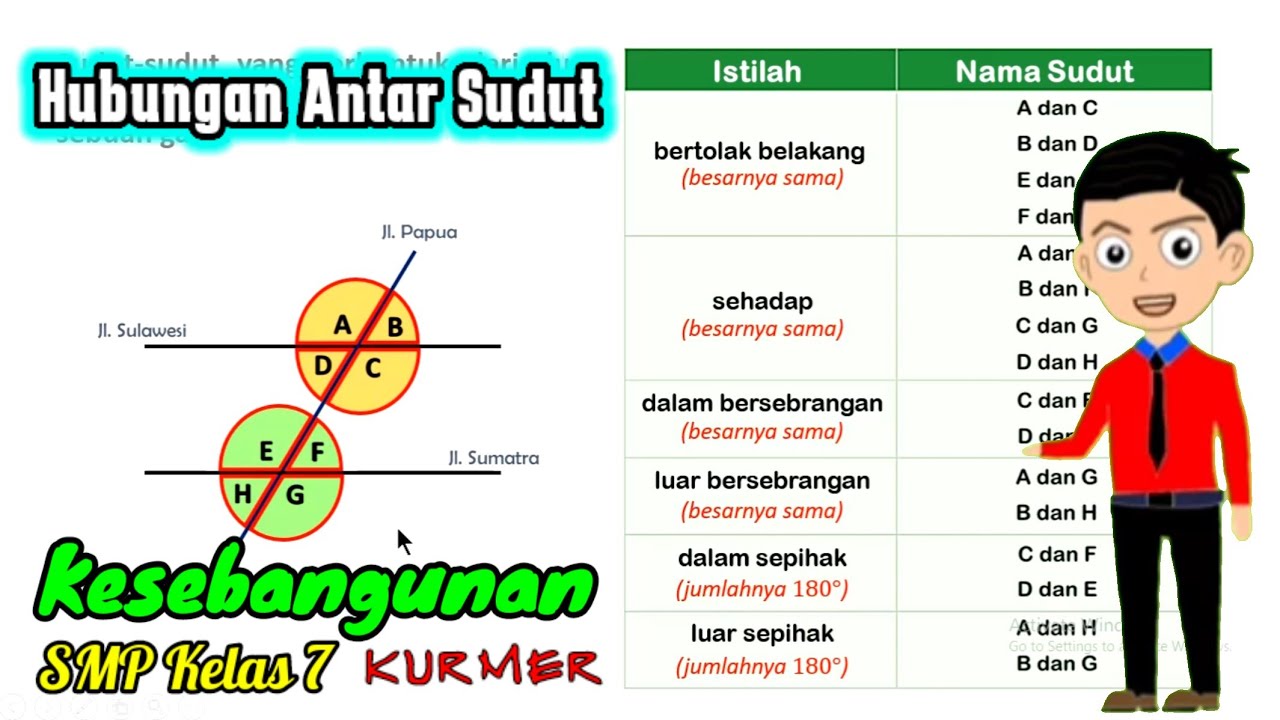
• 😀 Vertical angles (opposite angles) formed by intersecting lines are always equal in size.
• 😀 Adjacent angles are next to each other, and their sum can be important in solving problems.
• 😀 Complementary angles are pairs of angles that add up to 180°.
• 😀 Alternate interior and exterior angles formed by a transversal cutting parallel lines are equal.
• 😀 The importance of understanding how parallel and perpendicular lines affect angle relationships is emphasized.
• 😀 Practice problems are provided where students use geometric relationships to find unknown angles in various configurations.
• 😀 Creativity is encouraged in solving geometry problems, as geometric configurations can vary and require different strategies.

Q & A

What is the definition of a line in mathematics as discussed in the video?

In mathematics, a line is an undefined concept. It cannot be precisely defined but can be shown or illustrated. A line extends infinitely in both directions without any thickness.

What are the three types of relationships between two lines?

The three types of relationships between two lines are: intersecting lines, parallel lines, and skew lines. Intersecting lines meet at a point, parallel lines never meet and have the same direction, and skew lines neither meet nor are parallel, existing in different planes.

How can we differentiate between intersecting lines and skew lines?

Intersecting lines meet at a point, while skew lines do not meet and are not parallel. Skew lines lie in different planes, while intersecting lines lie in the same plane.

What does it mean for two lines to be parallel?

Two lines are parallel when, if extended indefinitely, they will never intersect. They always have the same direction and remain equidistant from each other.

What are adjacent angles?

Adjacent angles are two angles that share a common vertex and a common side but do not overlap. They are next to each other.

What is the relationship between complementary angles?

Complementary angles are two angles that add up to 90 degrees. When two angles form a right angle, they are complementary.

What are supplementary angles?

Supplementary angles are two angles that add up to 180 degrees. They form a straight line when placed together.

What are vertical angles, and what is their key property?

Vertical angles are the angles that are opposite each other when two lines intersect. These angles are always congruent, meaning they have equal measure.

How do you find the measure of an unknown angle when dealing with parallel lines and a transversal?

When parallel lines are cut by a transversal, various angle relationships, such as corresponding angles, alternate interior angles, and consecutive interior angles, can be used to find the measure of unknown angles. For example, corresponding angles are equal, and consecutive interior angles are supplementary.

What is the significance of creativity in solving geometric problems as mentioned in the video?

Creativity is important in solving geometric problems because it allows one to apply geometric principles in different ways. Sometimes, lines or angles may not be immediately obvious, so thinking creatively helps in using additional tools or drawing auxiliary lines to aid in solving problems.