Kinematika: Menentukan Kecepatan pada Mekanisme 4 Batang dengan Menggunakan Metode Kecepatan Relatif
Summary
TLDRThis video tutorial explains the process of determining velocities in a 4-bar mechanism using the relative velocity method. It guides viewers through the calculation of angular and linear velocities at different points in the system, utilizing graphical techniques like the Polygon of Velocities. Key steps include calculating the angular velocity of the rotating bars, finding the linear velocities of various points, and resolving vector directions. The tutorial also emphasizes common errors, such as incorrect placement of velocity vectors, and offers insights into accurately applying these concepts to solve kinematics problems in mechanical linkages.
Takeaways
- 😀 The script explains the process of determining relative velocities in a 4-bar mechanism, which is a fundamental topic in kinematics and mechanical design.
- 😀 The mechanism consists of four bars: one static (red), one rotating (green), and two connecting bars (yellow and purple).
- 😀 The primary focus is on calculating the angular velocity (ω) and linear velocity (v) at various points in the mechanism.
- 😀 The green bar rotates at 100 RPM (revolutions per minute), and the goal is to convert this into angular velocity in radians per second.
- 😀 Angular velocity is calculated using the formula: ω = (2 π * N) / 60, where N is the RPM.
- 😀 Linear velocity at point A on the second bar is determined by the formula: v = r * ω, where r is the length of the bar and ω is the angular velocity.
- 😀 The linear velocity at point A is found to be 0.523 m/s, and the direction of the velocity is illustrated graphically with respect to the rotation of the bars.
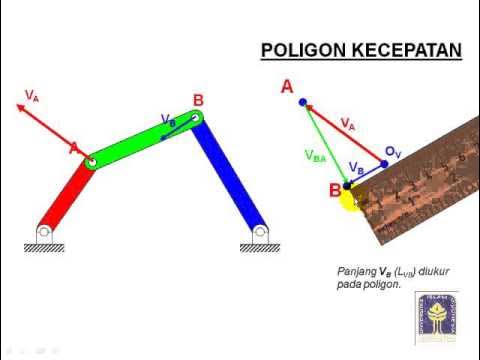
- 😀 A velocity polygon is used to determine the velocities of the other bars, ensuring accurate graphical representation of the magnitudes and directions of the velocities.
- 😀 The velocity polygon helps calculate the linear velocities at points B and C, as well as angular velocities of the third and fourth bars.
- 😀 The final results for the angular velocities of the third and fourth bars are 1.57 radians per second and 4.544 radians per second, respectively.
- 😀 The importance of accurately placing velocity vectors in the velocity polygon is emphasized to avoid mistakes in calculating the velocities, as misplacement can lead to incorrect results.
Q & A
What is the purpose of using the velocity polygon in kinematics?
-The velocity polygon is used to graphically determine the linear velocities of points on a mechanism. By placing the known velocities on the diagram and solving for unknown velocities, the method provides a clear visual representation of the system's kinematics.
How is angular velocity calculated in this 4-bar mechanism?
-Angular velocity (ω) is calculated using the formula: ω = (2π * N) / 60, where N is the rotational speed in RPM. In the given example, with a speed of 100 RPM for the green bar, the angular velocity for Bar 2 is found to be 10.46 radians per second.
What is the significance of the bar lengths in the calculations?
-The lengths of the bars are crucial because they are used in the formula for linear velocity (V = r * ω), where r is the length of the bar. This relationship allows us to calculate the linear velocities at specific points on the mechanism based on the angular velocities.
Why is it important to correctly place the velocity vectors in the velocity polygon?
-Correctly placing the velocity vectors is essential for accurate results. Misplacement can lead to incorrect calculations of velocities and angular velocities, as seen in the transcript where misplacement caused errors in the initial setup.
How do you determine the linear velocity at point A on Bar 2?
-The linear velocity at point A on Bar 2 is calculated by multiplying the radius (length of the bar) by the angular velocity. For Bar 2, with a radius of 50 mm and an angular velocity of 10.46 rad/s, the linear velocity at point A is found to be 0.523 m/s.
What does the term 'relative velocity' mean in the context of this mechanism?
-Relative velocity refers to the velocity of one point in relation to another. For example, the velocity of point B on Bar 3 is calculated relative to point A on Bar 2, as the motion of each point is influenced by the movement of connected bars.
What formula is used to calculate linear velocity in this system?
-Linear velocity is calculated using the formula V = r * ω, where V is the linear velocity, r is the length of the bar, and ω is the angular velocity. This formula is applied to various bars in the mechanism to determine the velocities at key points.
What were the key steps involved in solving for the velocity of point B on Bar 4?
-To solve for the velocity of point B on Bar 4, the velocity polygon method is used. First, the known velocity at point A is placed in the diagram. Then, the velocities for other points, such as B, are solved by constructing the polygon, resulting in the velocity of point B being 0.409 m/s.
How is the angular velocity of Bar 3 determined?
-The angular velocity of Bar 3 is determined after calculating the linear velocities at relevant points and using the formula V = r * ω. Once the linear velocity at point B on Bar 3 is known, the angular velocity (ω) is found to be 1.57 radians per second.
What happens if the relative velocity vectors are not placed correctly in the velocity polygon?
-If the relative velocity vectors are incorrectly placed, the calculated velocities will be inaccurate. For instance, placing the velocity vector at the wrong reference point can result in errors, leading to wrong values for both linear and angular velocities.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)