Calculate Normal Force On a Roller Coaster Cart | Circular Motion

Summary

In this video, the physics of a roller coaster is explored, focusing on two key points: the normal force acting on the cart as it passes through a trough (point A), and the maximum speed the cart can travel at the crest of a hill (point B) without losing contact with the track. The first part calculates the normal force at point A using centripetal force principles. The second part investigates the conditions under which the cart stays in contact with the track at the crest, determining the maximum speed for safe passage without the cart flying off the ramp.

Takeaways

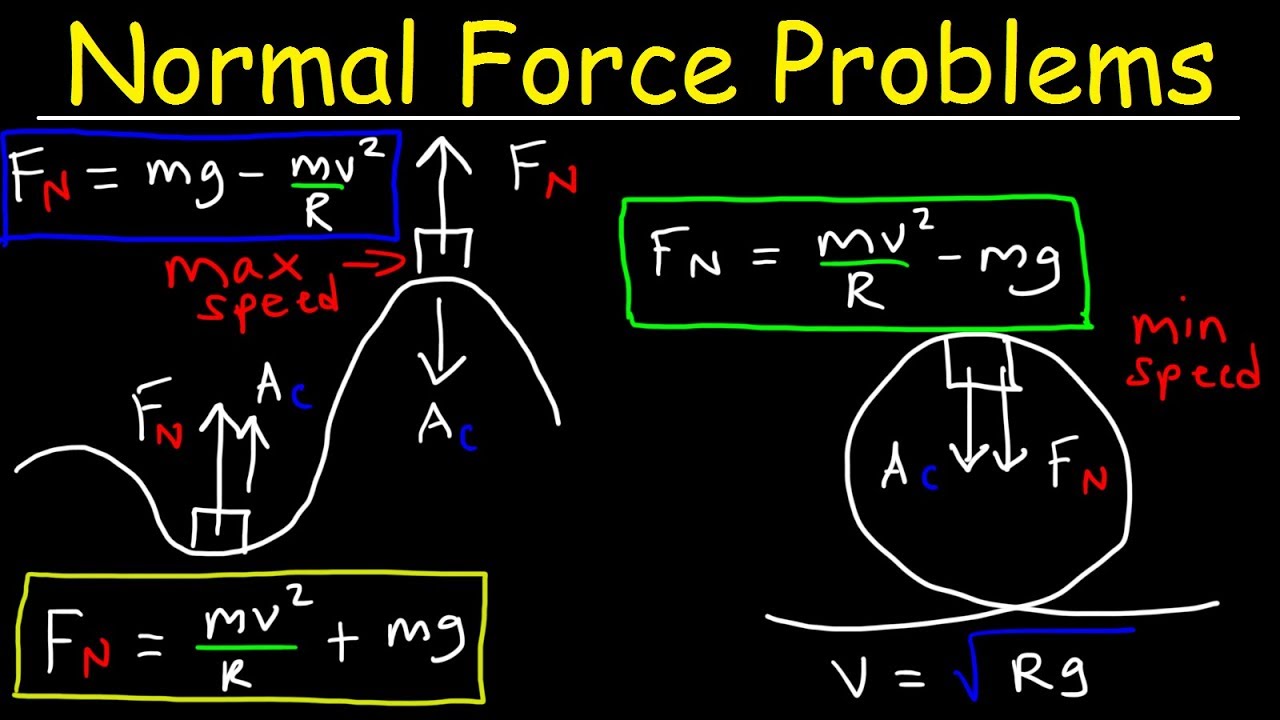
• 😀 The roller coaster car experiences two key forces as it moves: gravity acting downward and the normal force acting upward.
• 😀 The centripetal force is the net force that causes the roller coaster car to accelerate toward the center of the curve.
• 😀 At point A (the trough), the normal force and gravity combine to provide the necessary centripetal force.
• 😀 The normal force at point A is calculated to be 9116 newtons using the car's mass (250 kg), speed (20 m/s), and the radius of curvature (15 meters).
• 😀 At point B (the top of the hill), gravity still acts downward, but the car must maintain a certain speed to stay in contact with the track.
• 😀 If the car moves too fast over the crest of the hill, it will lose contact with the track and become airborne.
• 😀 At the critical speed for point B, the normal force becomes zero, and gravity alone provides the centripetal force required to keep the car on the track.
• 😀 The relationship between gravity and centripetal force at point B helps determine the maximum speed at which the cart can travel without flying off the track.
• 😀 The mass of the cart cancels out in the final equation for maximum velocity at point B, meaning it does not affect the result.
• 😀 The analysis of normal force, centripetal force, and gravity is crucial in understanding roller coaster dynamics and ensuring safety by preventing the cart from losing contact with the track.

Q & A

What is the main objective of the problem in the script?

The main objective is to solve for two things: (1) the normal force between the cart and the track at point A, and (2) the maximum speed at point B that will keep the cart in contact with the track.

Why is it important to consider both the normal force and gravity when analyzing the forces on the cart?

It's important because both forces act on the cart at the same time, and their combined effect determines the centripetal force that causes the cart to accelerate. Ignoring one of these forces would result in an incomplete analysis.

What role does the normal force play in this problem?

The normal force is the force exerted by the track on the cart, acting perpendicular to the surface of contact. It is crucial in determining the cart's motion and keeping it in contact with the track at point A.

What is the formula for centripetal force, and how is it used in this problem?

The formula for centripetal force is F_c = (mv^2) / r, where 'm' is the mass, 'v' is the velocity, and 'r' is the radius of curvature. This formula is used to calculate the net force required for the cart to follow the curved path.

How is the normal force at point A calculated?

The normal force at point A is calculated by considering the forces of gravity and the centripetal force. The equation F_n - mg = mv^2 / r is used, and after substituting the given values (mass = 250 kg, velocity = 20 m/s, radius = 15 m), the normal force is found to be 9116 N.

Why is the normal force at point B important?

At point B, the normal force is crucial to ensure that the cart stays in contact with the track. If the cart goes too fast, the normal force could be zero or negative, causing the cart to lose contact with the track and potentially fly off.

What happens if the cart moves too fast at point B?

If the cart moves too fast at point B, it will not stay in contact with the track and will effectively 'jump' off the track. This occurs when the normal force becomes zero or negative, meaning the centripetal force cannot be maintained.

What is the significance of free fall in the context of point B?

At point B, when the cart is moving at the right speed, it is in a state of free fall. This means that gravity is the only force acting on the cart, and the cart will move in such a way that the gravitational force provides the necessary centripetal force to keep it on the track.

How is the maximum velocity at point B calculated?

The maximum velocity at point B is calculated by equating the gravitational force to the centripetal force (F_gravity = F_centripetal). The equation is simplified to v_max = sqrt(r * g), where 'r' is the radius of curvature and 'g' is the acceleration due to gravity.

Why does the mass of the cart not affect the maximum speed at point B?

The mass of the cart cancels out in the equation when calculating the maximum speed at point B because both the gravitational force and the centripetal force depend on mass in the same way. Therefore, the mass does not influence the maximum velocity at the point where the cart is about to leave the track.