Usaha Energi Fisika Kelas 10 - Part 7 : Hukum Kekekalan Energi Mekanik

Summary

This video delves into the conservation of mechanical energy, specifically focusing on the law of conservation of mechanical energy and its applications. It explains how gravitational force, a conservative force, influences potential and kinetic energy in systems like a falling stone or a roller coaster. The presenter provides various examples, such as calculating speeds at different points in a roller coaster's loop and determining the minimum height required for a roller coaster to stay on track. Additional examples involving springs and free-falling objects further illustrate the principles of energy conservation, making it an insightful resource for physics learners.

Takeaways

• 😀 The law of conservation of mechanical energy states that the total mechanical energy of an object influenced by gravitational force remains constant, assuming only conservative forces (like gravity) are at play.
• 😀 When an object is dropped from a certain height, its potential energy is converted into kinetic energy as it falls, with potential energy being maximal at the highest point and kinetic energy being maximal at the lowest point.
• 😀 Mechanical energy consists of two components: potential energy (due to height) and kinetic energy (due to speed). These two energies transform into each other as the object moves.
• 😀 In conservative systems, where only conservative forces act (like gravity), the total mechanical energy at the beginning equals the total mechanical energy at the end, represented by the equation: E_initial = E_final.
• 😀 In the case of a pendulum, the tension in the string is a non-conservative force, but since it acts perpendicular to the motion, it does no work and does not affect the total mechanical energy.
• 😀 In roller coaster problems, the mechanical energy at various points on the track is used to calculate the velocity of the roller coaster at those points, assuming no friction or non-conservative forces.
• 😀 For roller coasters with vertical loops, conservation of mechanical energy can be used to find speeds at different points on the loop, with gravitational potential energy converting to kinetic energy and vice versa.
• 😀 To keep a roller coaster on track at the top of a loop, the normal force acting on the roller coaster must be at least zero, which ensures that it doesn’t fall off the track.
• 😀 The minimum height required for a roller coaster to maintain a circular motion without falling off the track is derived from the conservation of mechanical energy and the condition for zero normal force at the highest point.
• 😀 For problems involving a spring and an object, the mechanical energy is conserved as the object moves. The spring’s potential energy converts into the object’s kinetic energy, and this principle can be used to calculate velocities and distances.
• 😀 In the case of objects falling from a height onto a spring, the velocity of the object just before hitting the spring can be found using energy conservation principles, and the maximum compression of the spring can be calculated by equating the mechanical energies at different points.

Q & A

What is the law of conservation of mechanical energy?

The law of conservation of mechanical energy states that the total mechanical energy of an object, influenced by gravitational force (a conservative force), remains constant, provided there are no non-conservative forces like friction doing work on the object.

What are the components of mechanical energy?

Mechanical energy consists of two main components: potential energy (due to an object's height or position) and kinetic energy (due to an object's motion).

In the example of a stone being dropped from a height, how does energy transformation occur?

When the stone is dropped, its potential energy is converted into kinetic energy. At the highest point, the potential energy is maximal, and kinetic energy is zero. As it falls, potential energy decreases, and kinetic energy increases. At the lowest point, the potential energy is zero, and the kinetic energy is maximal.

Why can the tension force in a pendulum be considered non-conservative, yet the law of conservation of energy still applies?

The tension force in the pendulum is considered non-conservative because it does no work on the object. The tension force is perpendicular to the motion, meaning it does not affect the mechanical energy. Therefore, only the gravitational force, a conservative force, contributes to the energy conservation.

What is the equation for mechanical energy conservation in the case of conservative forces?

The equation for mechanical energy conservation is: E_initial = E_final, which can be expanded as (Ep1 + Ek1 = Ep2 + Ek2), where Ep represents potential energy and Ek represents kinetic energy at two points in the system.

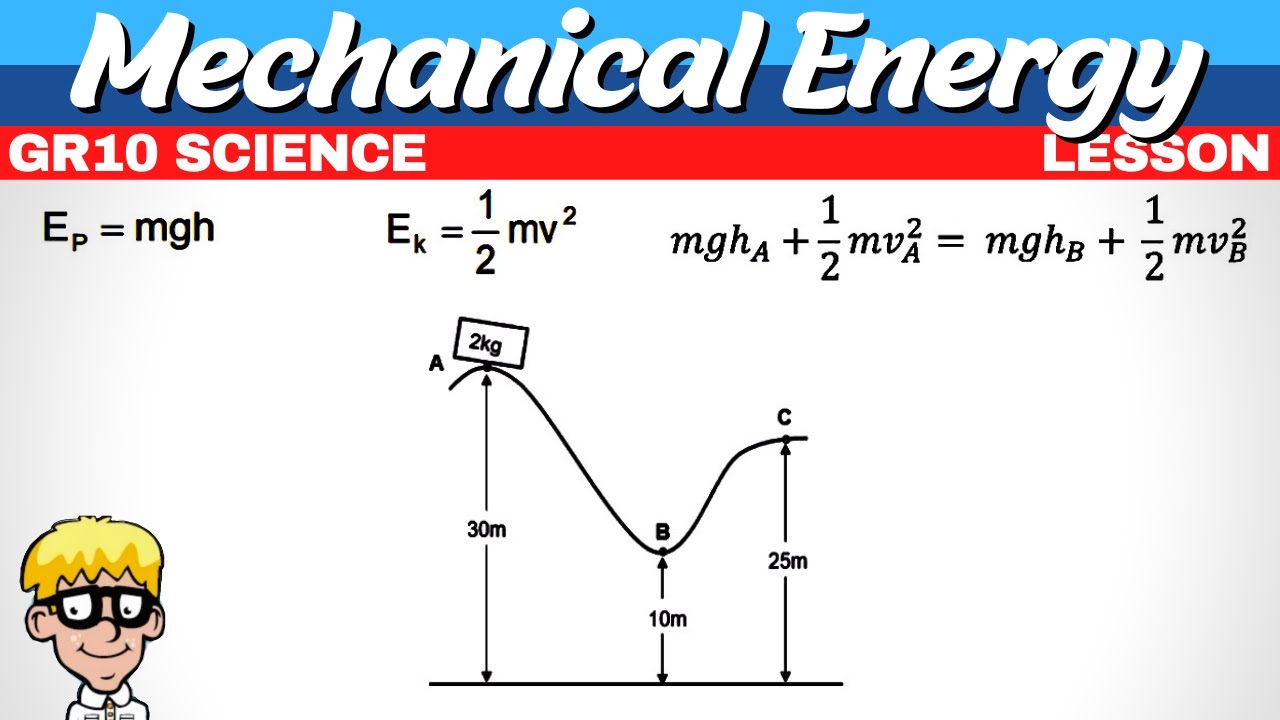
In the roller coaster example, what does the law of conservation of mechanical energy help calculate?

The law of conservation of mechanical energy in the roller coaster example helps calculate the speed of the coaster at different points on the track, such as at points B, C, and D, assuming no friction or non-conservative forces are acting.

How do you calculate the velocity at point B in the roller coaster example?

To calculate the velocity at point B, you apply the energy conservation principle. At point A, the mechanical energy is entirely potential energy (mgh), and at point B, it’s entirely kinetic energy (1/2 m * vB^2). By equating the two energies, you solve for vB, yielding the formula vB = √(2gh).

Why is the minimum height (H) for the roller coaster crucial for the coaster to stay on the track?

The minimum height ensures that the coaster has enough potential energy to maintain motion through the loop. If the coaster’s velocity becomes zero or if the normal force at the top of the loop goes to zero, it will not stay on the track. The height calculation ensures that the coaster can maintain the necessary speed at the top of the loop.

How is the velocity at point C in the roller coaster problem calculated?

To calculate the velocity at point C, you apply the energy conservation equation between points B and C. Since there is no potential energy at point B (height is zero), the total mechanical energy is purely kinetic. The energy at point C includes both potential energy (mg * 2R) and kinetic energy (1/2 m * vc^2), allowing you to solve for vc.

In the spring compression problem, how do you determine the speed of the object before it reaches the spring?

To find the speed of the object before it reaches the spring, you use the law of conservation of mechanical energy. The initial energy is stored as potential energy in the compressed spring, and when the spring is released, it is converted into the object's kinetic energy. The formula 1/2 k * Δx^2 = 1/2 m * v^2 is used to solve for the velocity.