La elipse con centro en el origen. Introducción y ejemplo 1.
Summary
TLDREn este video se explica detalladamente el concepto de la elipse, sus elementos fundamentales como los focos, el centro, los vértices, y los ejes mayor y menor. Se presenta la fórmula general para la ecuación de la elipse, tanto horizontal como vertical, y se resuelve un ejercicio práctico donde se encuentran la ecuación ordinaria y general de una elipse, así como propiedades como los focos, la excentricidad y el lado recto. La explicación incluye un bosquejo visual y cálculos paso a paso para comprender cómo aplicar estos conceptos en ejercicios matemáticos.
Takeaways
- 😀 Una elipse está definida por dos focos fijos, el centro y los vértices, y tiene dos ejes: el mayor (eje horizontal) y el menor (eje vertical).
- 😀 La distancia desde el centro hasta cada foco se representa con la letra 'c', y la distancia desde el centro hasta los vértices se representa con la letra 'a'.
- 😀 Los vértices de una elipse están ubicados sobre el eje mayor, mientras que el eje menor se extiende perpendicularly.
- 😀 En el caso de una elipse horizontal, los focos se ubican en el eje x, y en una elipse vertical, los focos se encuentran en el eje y.
- 😀 La excentricidad de una elipse mide cuán achatada es; cuanto más cercana a 0, más parecida es a una circunferencia.
- 😀 El lado recto de la elipse es la distancia entre los extremos, pasando por el foco, y se calcula como 2b²/a.
- 😀 Se puede aplicar el teorema de Pitágoras para despejar valores desconocidos en una elipse, como la distancia de los focos (c).
- 😀 La ecuación ordinaria de una elipse horizontal se puede escribir como x²/a² + y²/b² = 1, mientras que para una elipse vertical se invierten las posiciones de 'a' y 'b'.
- 😀 En el ejemplo proporcionado, para una elipse con centro en el origen y vértices en (5,0) y (-5,0), la ecuación ordinaria resultante es x²/25 + y²/16 = 1.
- 😀 El eje mayor se calcula como 2a, y en el ejemplo, si a=5, entonces el eje mayor es 10.
- 😀 El ejercicio también incluye cálculos adicionales como la excentricidad (3/5), el lado recto (32/5), y la identificación de los focos, que son (3,0) y (-3,0).
Q & A
¿Qué es una elipse y cuáles son sus elementos principales?
-Una elipse es una curva plana cerrada que tiene varios elementos clave: dos puntos fijos llamados focos (fox), el centro de la elipse, los vértices que están en los extremos de la elipse, y los ejes mayor y menor que definen su forma.
¿Cómo se definen las coordenadas de los focos en una elipse horizontal?
-En una elipse horizontal, los focos están situados a una distancia 'c' del centro a lo largo del eje X. Así, sus coordenadas son (c, 0) y (-c, 0).
¿Qué diferencia existe entre una elipse horizontal y una vertical?
-En una elipse horizontal, los vértices están sobre el eje X, y el eje mayor es horizontal. En una elipse vertical, los vértices están sobre el eje Y, y el eje mayor es vertical. La forma de la elipse cambia según la orientación de estos ejes.
¿Cómo se calcula la distancia 'c' entre el centro y los focos?
-La distancia 'c' se calcula usando el teorema de Pitágoras: c^2 = a^2 - b^2, donde 'a' es la distancia del centro al vértice (semi-eje mayor) y 'b' es la distancia del centro al extremo del eje menor.
¿Qué es la excentricidad de una elipse?
-La excentricidad de una elipse mide qué tan achatada es. Se calcula como e = c/a, donde 'c' es la distancia del centro a un foco, y 'a' es el semi-eje mayor. Cuanto más cercana a 0 sea la excentricidad, más circular es la elipse.
¿Cómo se calcula el lado recto de una elipse?
-El lado recto es la distancia entre los extremos de la elipse, pasando por uno de los focos. Se calcula como 2b^2/a, donde 'b' es el semi-eje menor y 'a' es el semi-eje mayor.
¿Qué es el eje mayor y cómo se calcula?
-El eje mayor es la línea más larga de la elipse, que pasa por los vértices. Se calcula como 2a, donde 'a' es la distancia desde el centro hasta uno de los vértices en el eje mayor.
¿Cómo se determina la ecuación ordinaria de una elipse?
-La ecuación ordinaria de una elipse se escribe como (x^2/a^2) + (y^2/b^2) = 1, donde 'a' es el semi-eje mayor y 'b' el semi-eje menor. Esta fórmula se obtiene sustituyendo los valores de 'a' y 'b' en la ecuación estándar.
¿Cuál es la diferencia entre la ecuación ordinaria y la ecuación general de una elipse?
-La ecuación ordinaria está en la forma (x^2/a^2) + (y^2/b^2) = 1, mientras que la ecuación general tiene la forma Ax^2 + By^2 + C = 0, y se obtiene multiplicando la ecuación ordinaria por los denominadores de 'a^2' y 'b^2' y reorganizando los términos.
En el ejemplo dado, ¿cuáles son los focos y sus coordenadas?
-En el ejemplo, los focos están en las coordenadas (3, 0) y (-3, 0), ya que la distancia 'c' es 3 y están ubicados a lo largo del eje X.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

🏉 ELIPSE: Concepto y elementos (focos, vértices, Eje Mayor, Eje Menor, L.R.) | Juliana la profe
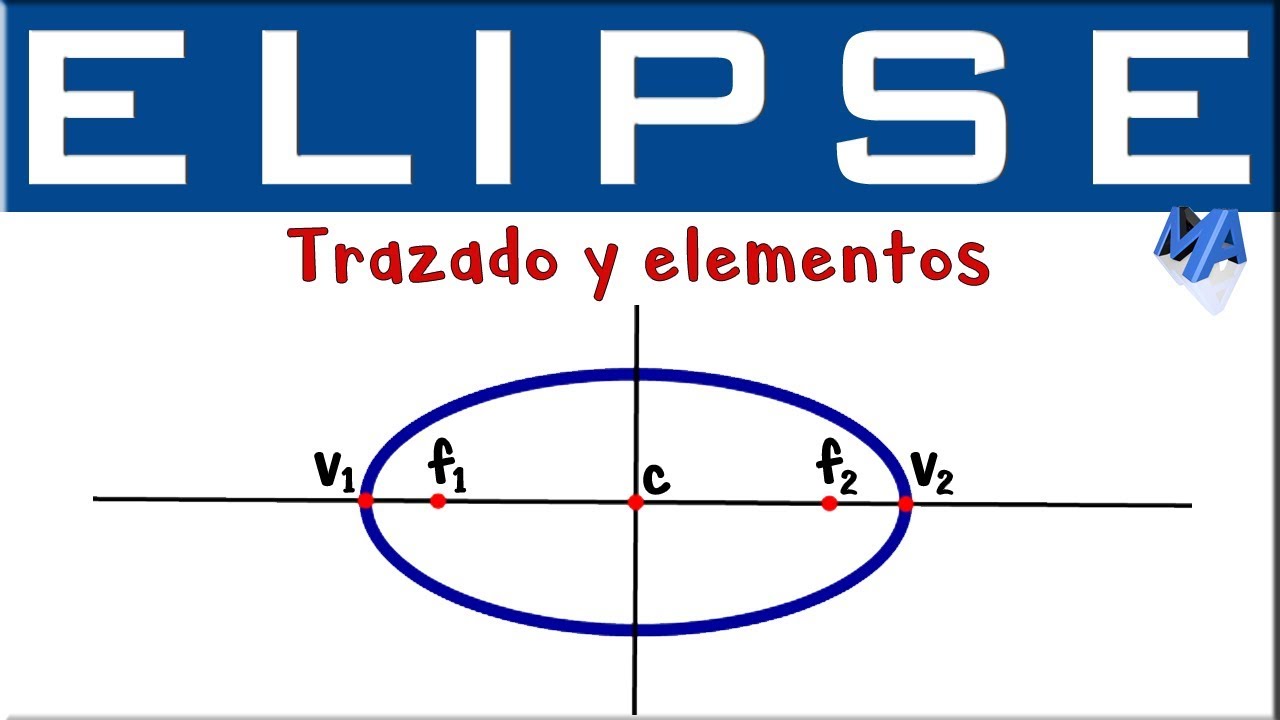
Elipse trazado y elementos | Introducción

✅ELIPSE con centro FUERA del ORIGEN [100% 𝙀𝙛𝙚𝙘𝙩𝙞𝙫𝙤 😎🫵💯] Geometría Analítica

Gráfica y elementos de la Elipse conociendo la ecuación canónica | Ejemplo 1

Las Cónicas (teoría).

Geometría Analítica: Ecuación de la elipse dados foco y la excentricidad.
5.0 / 5 (0 votes)
