0625 Distribución binomial
Luis Rincón
15 Dec 201329:18
Takeaways
- 😀 二項分布は、独立したベルヌーイ試行における成功の回数をモデル化する離散確率分布です。
- 😀 成功の確率をp、失敗の確率を1-pとしたn回の試行を考え、成功回数Xが0からnまでの値を取ることができます。
- 😀 二項分布の確率質量関数は、P(X = x) = (nCx) p^x (1-p)^(n-x)で表され、xは成功の回数です。
- 😀 二項分布の期待値(平均)はE[X] = n * p、分散はVar(X) = n * p * (1 - p)です。
- 😀 累積分布関数(CDF)は、Xがx以下の値を取る確率を示し、個別の確率を合計することで計算されます。
- 😀 二項分布の関数生成器は、確率生成器として使われ、t^Xの期待値を求めることで得られます。
- 😀 変換された累積分布や生成関数の計算において、独立した確率変数の利用が重要な役割を果たします。
- 😀 二項分布は、n回の独立した試行において成功回数を予測するため、品質管理や確率論的な問題に広く利用されます。
- 😀 例として、100個のうち7%が欠陥品の時、サンプル5個を無作為に選び、そのうち少なくとも1つが欠陥品である確率を求める問題があります。
- 😀 確率計算において、補数の法則を使うことで、P(X >= 1) = 1 - P(X = 0)とし、効率よく結果を得ることができます。
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Las distribuciones Bernoulli, binomial y normal
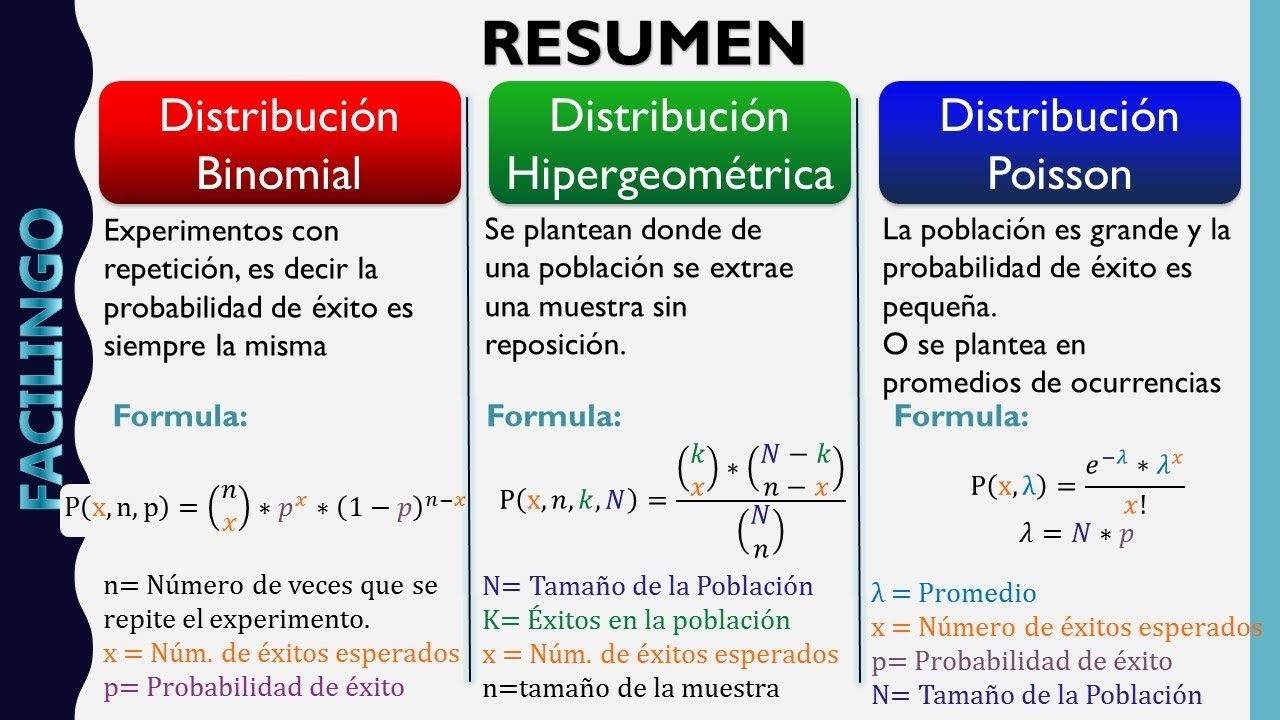
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

02 Distribución binomial. Función de probabilidad

03 Problemas de distribución binomial

Distribución binomial | Ejercicio resuelto 2: representación mediante tabla y gráfica

Distribución Hipergeométrica

Distribución binomial | Ejercicios resueltos | Introducción
Rate This
★
★
★
★
★
5.0 / 5 (0 votes)
関連タグ
二項分布確率論ベルヌーイ期待値分散確率関数実例数学統計学確率計算