Secant Method | Numerical Methods
Summary
TLDRIn this video, the secant method for finding roots of non-linear equations is explained. It’s an open method similar to Newton’s method, but relies on two initial guesses instead of one. The video covers the steps involved: choosing initial x-values, using a Taylor series expansion to approximate a secant line, finding where the secant line crosses the x-axis, and iterating the process until convergence. The secant method is noted for its stability and slower pace compared to Newton’s method. Viewers are encouraged to select initial guesses carefully for better convergence and reliability.
Takeaways
- 😀 The secant method is an open root-finding method used to solve non-linear equations.
- 😀 It is similar to Newton's method, but differs in that it uses two initial guesses instead of one.
- 😀 The secant method relies on first-order Taylor series expansion to approximate the function with a secant line.
- 😀 The key steps in the secant method include selecting two initial estimates and iterating until the root is found.
- 😀 In step one, two initial x-values are chosen based on where you think the root lies.
- 😀 In step two, a Taylor series is used to approximate the function and create a secant line.
- 😀 In step three, the secant line's intersection with the x-axis is found, providing the next estimate for the root.
- 😀 The secant method repeats the previous two steps, refining the estimate with each iteration until the result is sufficiently close to the true root.
- 😀 Unlike Newton's method, the secant method does not require the derivative of the function, making it more versatile.
- 😀 The secant method is more stable than Newton’s method because it uses two initial guesses, but it may be slower.
- 😀 It’s important to choose initial guesses carefully—picking values near the root from a graph can improve convergence speed and reliability.
Q & A
What is the secant method used for?
-The secant method is an open root-finding method used to find the roots of non-linear equations.
How is the secant method related to Newton's method?
-The secant method is similar to Newton’s method, with the key difference being that Newton’s method relies on a single initial guess, while the secant method uses two initial guesses.
What is the first step in implementing the secant method?
-The first step is to pick two initial x-values, which are estimates of where the root is likely to be.
What does the first order Taylor series expansion do in the secant method?
-The first order Taylor series expansion is used to approximate a function for the secant line, which helps in finding the root of the non-linear equation.
Why are Taylor series expansions useful in the secant method?
-Taylor series expansions are useful because they approximate continuous functions as polynomials, and the derivatives of polynomials are easier to compute, which simplifies the process of finding the root.
What is the purpose of finding the secant line’s intersection with the x-axis?
-The purpose is to find the x-value where the secant line crosses the x-axis, which gives the next x-value (iteration) in the secant method.
How do you calculate the error in the secant method?
-The error is calculated by taking the difference between the current x-value and the previous x-value in the iteration process.
What is the biggest advantage of the secant method over Newton's method?
-The biggest advantage of the secant method is its stability, as it uses two initial guesses, making it more reliable in finding the root compared to Newton’s method, which relies on just one guess.
Why is it important to not randomly select initial guesses in the secant method?
-It is important to avoid randomly selecting initial guesses because picking values too far from the actual root can slow down convergence and make the method less reliable. It's recommended to use a graph to select appropriate initial guesses near the root.
What is the trade-off when using the secant method compared to Newton's method?
-The trade-off is that the secant method, while more stable due to using two initial guesses, tends to be slightly slower than Newton's method, which only requires one initial guess.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Bisection Method | Numerical Methods
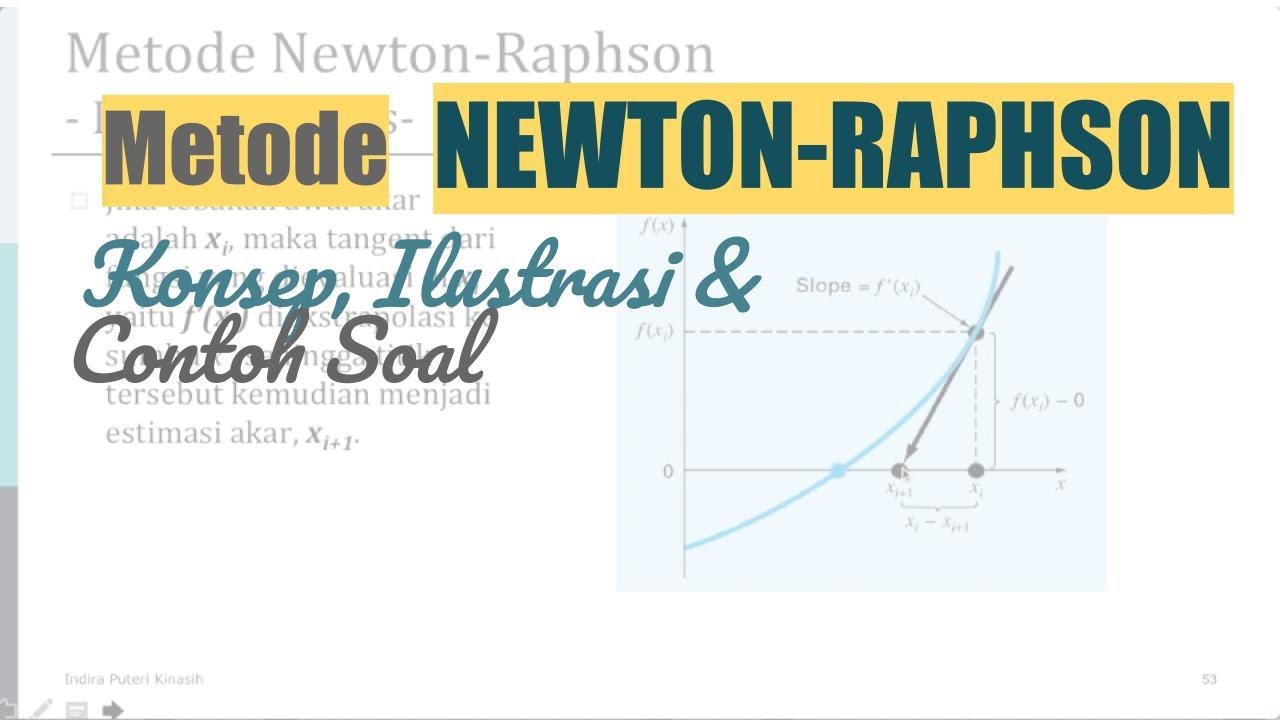
Metode Newton Raphson (Konsep & Contoh) [Metode Numerik]

8. METODE LELARAN TITIK TETAP - FIX POINT ITERATION - METODE NUMERIK

METODE NUMERIK P7 PART 1/2 | METODE NEWTON-RAPHSON UNTUK MENYELESAIKAN PERSAMAAN NON LINIER
5 MTK EKO PENCARIAN AKAR AKAR PERS LINEAR

Zeros de funções Método Iterativo Linear
5.0 / 5 (0 votes)
