Modelo McCulloch y Pitts: La primer neurona artificial
Summary
TLDREn esta sesión, se explora la red neuronal de McCulloch y Pitts, considerada la primera modelo de neurona artificial, propuesta en 1943. La discusión se enfoca en la estructura binaria y el comportamiento de todo o nada de la neurona, así como en las entradas excitatorias e inhibitorias que determinan su activación. Se describen las reglas que gobiernan el funcionamiento de la neurona y cómo, a través de un umbral, se decide su salida. Además, se menciona la limitación del modelo para representar pensamientos complejos y su relevancia histórica en el campo de la inteligencia artificial. La sesión concluye con una breve mención del modelo del perceptrón y se anuncia la programación del modelo de McCulloch-Pitts en Python en una futura sesión.
Takeaways
- 👋 Hola a todos, en esta sesión se discute sobre la red neuronal más antigua propuesta por McCulloch y Pitts.
- 🧠 McCulloch tenía formación en neurociencias y Pitts en matemáticas, lo que les permitió crear un modelo de neurona que intentaba explicar la generación del pensamiento a partir de impulsos físicos.
- 📈 El modelo de McCulloch-Pitts es un modelo matemático que, bajo ciertas restricciones, puede generar premisas verdaderas o falsas, representando pensamientos.
- 🚫 Aunque el modelo no explica directamente cómo funciona el cerebro humano, fue un avance importante en la comprensión de cómo podrían funcionar las neuronas.
- 🔢 Las entradas y salidas del modelo son binarias, lo que significa que solo pueden ser 0 (desactivada) o 1 (activada).
- ⚖️ Se define un umbral (un valor natural) que determina si la neurona se activa o no basado en la suma de las entradas excitatorias.
- 🏛 El comportamiento de la neurona se rige por dos reglas principales: si hay una entrada inhibitoria activa, la salida es cero; si no, se evalúa la suma de las entradas excitatorias contra el umbral.
- 🔴 La neurona de McCulloch-Pitts puede representar funciones lógicas básicas como OR, AND y NOT.
- 🤖 El potencial de las redes neuronales McCulloch-Pitts yace en la capacidad de tener un conjunto de neuronas interconectadas para procesamientos más complejos.
- ⏱ El modelo también consideraba el tiempo que toma el proceso de inferencia y la estabilización de valores en las neuronas.
- 📉 El modelo de McCulloch-Pitts cayó en desuso debido a su simplicidad y la dificultad para entrenar las neuronas con la función de activación que utilizaban.
- 🚀 Se menciona que en una próxima sesión se programará el modelo de McCulloch-Pitts en Python para entender mejor su funcionamiento y aplicaciones.
Q & A
¿Quiénes fueron los científicos que propusieron la red neuronal más antigua de la que se tiene reporte?
-La red neuronal más antigua fue propuesta por Warren Sturgis McCulloch y Walter Pitts.
¿En qué año fue publicado el artículo que reporta la red neuronal de McCulloch y Pitts?
-El artículo que reporta la red neuronal de McCulloch y Pitts fue publicado en 1943.
¿Cuál es la formación académica de McCulloch y en qué campo se especializó?
-McCulloch tenía formación en neurociencias, con estudios en biología y matemáticas, y su campo de estudio se centraba en cómo se genera el pensamiento a partir de los impulsos físicos.
¿Cómo se define el comportamiento de las neuronas en el modelo de McCulloch y Pitts?
-En el modelo de McCulloch y Pitts, las neuronas tienen un comportamiento de todo o nada, es decir, se activan o no activan en función de las entradas que reciben.
¿Cuáles son las dos clases de entradas que consideran en el modelo de McCulloch y Pitts?
-Las dos clases de entradas en el modelo de McCulloch y Pitts son las entradas excitatorias, representadas con una 'E' mayúscula, y las entradas inhibitorias, representadas con una 'I'.
¿Cómo se define el umbral en el modelo de McCulloch y Pitts?
-El umbral en el modelo de McCulloch y Pitts es un elemento extra que puede tener valores naturales o positivos, incluido el cero, y que determina si la neurona se activa o no en función de las entradas recibidas.
¿Qué sucede si existe una entrada inhibitoria activa en la neurona de McCulloch y Pitts?
-Si existe una entrada inhibitoria activa, la salida de la neurona es cero, independientemente de las otras entradas.
¿Cómo se calcula la salida de una neurona de McCulloch y Pitts si no hay entradas inhibitorias activas?
-Si no hay entradas inhibitorias activas, se calcula la suma de todas las entradas excitatorias. Si la suma es mayor o igual al umbral, la salida es uno; de lo contrario, es cero.
¿Por qué el modelo de McCulloch y Pitts entró en desuso y fue reemplazado por el modelo del perceptrón?
-El modelo de McCulloch y Pitts entró en desuso debido a su limitación de ser un sistema binario de todo o nada, lo que dificultaba la representación de valores reales. Además, los métodos para entrenar estas neuronas eran relativamente estancados y se dificultaba inferir cambios para obtener una salida deseada. Con el tiempo, la electrónica analógica permitió representar valores reales, lo que llevó al desarrollo del modelo del perceptrón.
¿Qué tipo de compuertas lógicas podrían representar las neuronas de McCulloch y Pitts?
-Las neuronas de McCulloch y Pitts podrían representar una variedad de compuertas lógicas, incluyendo OR, AND y NOT.
¿Cuál es la principal limitación del modelo de McCulloch y Pitts en términos de su capacidad para representar pensamientos o procesos cerebrales?
-La principal limitación del modelo de McCulloch y Pitts es su simplicidad y el hecho de ser un modelo binario de todo o nada, lo que no es capaz de representar la complejidad y la continuidad de los procesos neuronales en el cerebro humano.
¿Cómo se podría mejorar el modelo de McCulloch y Pitts para representar valores no binarios?
-Para representar valores no binarios, se podrían incorporar pesos en las entradas,允许它们采取非二进制值,从而允许更复杂的数学运算和更精细的神经元激活控制。
¿Por qué es importante la implementación del modelo de McCulloch y Pitts en un programa de Python?
-La implementación del modelo de McCulloch y Pitts en Python es importante porque permite a los estudiantes y profesionales entender mejor el funcionamiento del modelo a través de la práctica, además de facilitar la creación de prototipos y experimentos para el estudio y la mejora de redes neuronales.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
Neurona de McCulloch y Pitts programada en Python

La EVOLUCIÓN de la Inteligencia Artificial 🤖 El Desarrollo de la IA en la HISTORIA🧩

The Stilwell Brain

Bomba sodio-potasio | Biología humana | Biología | Khan Academy en Español
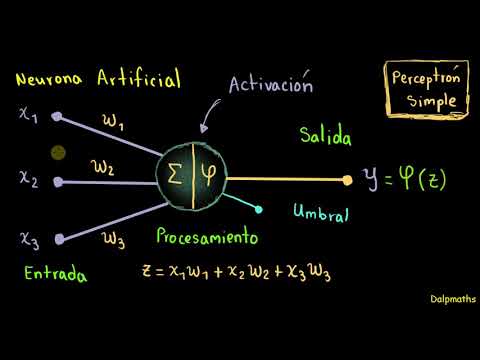
Redes neuronales: Introducción al perceptrón simple.

Curso de Redes 1.5. El modelo TCP/IP y su arquitectura.
5.0 / 5 (0 votes)
