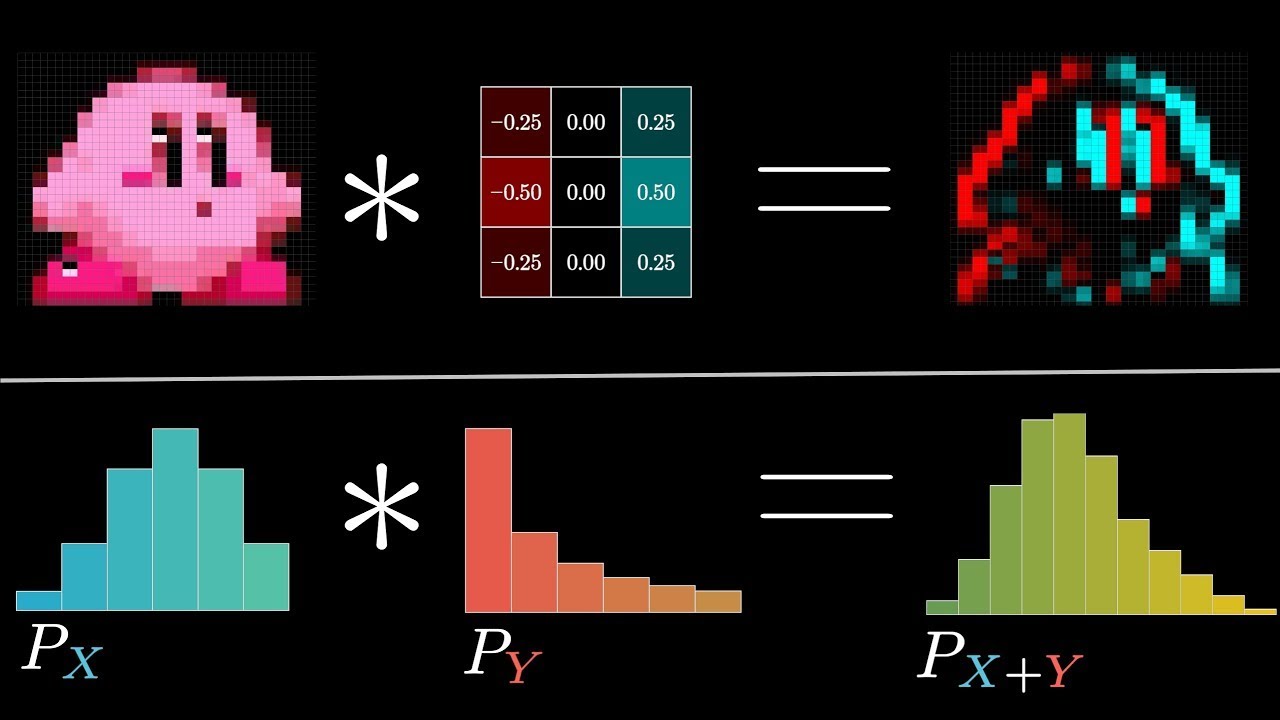
Distribución beta.

Summary

このビデオでは、ベータ分布とその確率論における応用について学びます。特に、メキシコにおける致命的な交通事故の割合をモデリングするためのベータ分布の使用法が説明されています。ベータ分布の確率密度関数（PDF）の導出方法、ガンマ関数との関連、および確率計算の具体的な例（事故の割合が特定の範囲内にある確率の計算）を通じて、比例に基づくモデルの理解が深まります。

Takeaways

• 😀 ベータ分布を理解する前に、ベータ関数の定義と性質を確認する必要がある。
• 😀 ベータ関数は、アルファとベータのパラメータに対して、積分によって計算される。
• 😀 ベータ関数とガンマ関数との間には密接な関係があり、ガンマ関数を使うことで計算が簡便になる。
• 😀 ベータ分布の確率密度関数は、0から1の範囲で定義され、アルファとベータのパラメータによって形状が決まる。
• 😀 ベータ分布は比例（0〜1の範囲の値を取る）のデータをモデル化するのに適している。
• 😀 例として、メキシコでの致命的な交通事故の割合がベータ分布でモデル化されることが示された。
• 😀 ベータ分布の確率密度関数は、特定のアルファとベータに基づき具体的な数式が得られる。
• 😀 事故の割合が40%未満である確率を計算するためには、確率密度関数の積分を使って求める。
• 😀 積分の結果、40%未満の確率が66.3%であることが示され、ベータ分布の活用方法が明示された。
• 😀 25%と50%の間で事故の致命的な割合がある確率を計算することで、ベータ分布の応用例がさらに深く理解できる。