Coeficiente de correlación. Ejercicio 1
Summary
TLDREste video explica cómo calcular el coeficiente de correlación utilizando una muestra de datos. Se detalla el proceso que incluye la obtención de la media aritmética, varianza y covarianza de las variables observadas. Se enfatiza la importancia de utilizar herramientas visuales, como ventanas, para facilitar la comprensión de los cálculos. Además, se aclara que el coeficiente de correlación, que no debe exceder uno en valor absoluto, es crucial para el análisis estadístico. Al final, se da un consejo sobre la presentación escrita para evitar problemas en la evaluación por parte de los profesores.
Takeaways
- 📊 El coeficiente de correlación se calcula como el cociente entre la covarianza de la muestra y el producto de las desviaciones típicas.
- 📈 La media aritmética de la variable X se obtiene mediante la fórmula adecuada para los valores observados.
- 📉 La varianza se determina utilizando el cuadrado de la media aritmética de la muestra.
- 🔍 La covarianza se calcula utilizando las frecuencias observadas de las variables X e Y.
- 🔑 Es fundamental comprender el significado y la importancia del coeficiente de correlación en análisis estadísticos.
- 📋 Se recomienda utilizar 'ventanas' para facilitar la organización y lectura de los cálculos.
- ✅ La suma de las frecuencias absolutas de X e Y debe ser igual al tamaño de la muestra.
- ⚖️ Los datos no agrupados en intervalos permiten un cálculo directo del coeficiente de correlación.
- 📉 El coeficiente de correlación siempre tiene un valor absoluto menor o igual a uno.
- ✏️ Una presentación clara y legible en los exámenes es crucial para evitar problemas con los profesores.
Q & A
¿Qué información se proporciona sobre la muestra en el video?
-Se proporciona información sobre las frecuencias absolutas observadas de las variables X e Y, así como el tamaño total de la muestra, que es 9.
¿Cómo se calcula el coeficiente de correlación?
-El coeficiente de correlación se calcula como el cociente entre la covarianza de la muestra y el producto de las desviaciones típicas de las variables X e Y.
¿Cuál es la media aritmética de la variable X?
-La media aritmética de la variable X es 1.
¿Qué varianza tiene la muestra de la variable Y?
-La varianza de la muestra de la variable Y es 36.81.
¿Qué valor se obtiene para la covarianza de la muestra?
-El valor de la covarianza correspondiente a la muestra es -1.81.
¿Cuál es la relación entre la covarianza y el coeficiente de correlación?
-La covarianza es un componente necesario para calcular el coeficiente de correlación, que indica la dirección y fuerza de la relación entre las variables.
¿Por qué es importante el uso de 'ventanas' al presentar cálculos estadísticos?
-El uso de 'ventanas' facilita la lectura y comprensión de los cálculos realizados, lo que puede ser apreciado por los profesores.
¿Qué se menciona sobre la agrupación de datos en intervalos?
-Se menciona que si los datos de X o Y estuvieran agrupados en intervalos de clase, se usarían marcas de clase como datos representativos para calcular la covarianza.
¿Qué se debe recordar acerca del valor absoluto del coeficiente de correlación?
-El valor absoluto del coeficiente de correlación no debe ser superior a uno, lo cual es cierto para todas las muestras.
¿Qué consejo se da sobre la presentación escrita en los exámenes?
-Se aconseja tener una letra clara, ya que una mala presentación puede influir negativamente en la percepción que los profesores tengan de los exámenes.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Coeficiente de Correlación

Pensamiento matemático. Progresión 9. Calcular coeficiente de correlación en Excel

Análisis de correlación con Excel

Rango, varianza, desviación estándar, coeficiente de variación, desviación media: datos no agrupados
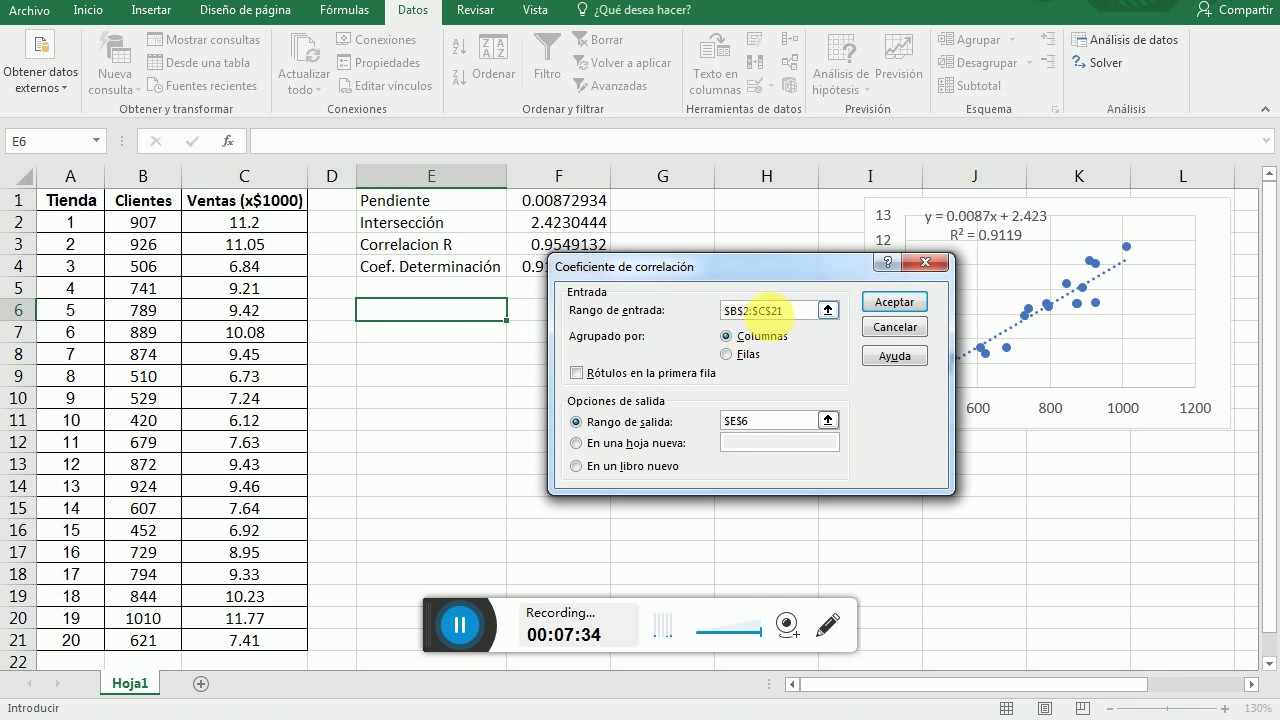
Sección 2.12 Ejercicio 01. Regresión y correlación en Excel

Estadística Datos Bivariados
5.0 / 5 (0 votes)
