Cuartil, Decil y Percentil para Datos No Agrupados.
Summary
TLDREn este video se explora el cálculo de cuartiles y percentiles utilizando datos no agrupados, específicamente las edades de los trabajadores de una microempresa. Se explica la importancia de organizar los datos y se presentan fórmulas claras para calcular el tercer cuartil y el percentil 40. A través de ejemplos prácticos, se ilustra cómo manejar situaciones con datos decimales y realizar interpolaciones, asegurando una comprensión profunda de las técnicas estadísticas. Este contenido es ideal para quienes desean mejorar su conocimiento en análisis de datos.
Takeaways
- 😀 Es importante organizar los datos antes de realizar cualquier cálculo estadístico.
- 📊 Los cuartiles son valores que dividen un conjunto de datos en cuatro partes iguales.
- 🔢 Para calcular el cuartil 3, se utiliza una fórmula específica que depende de si el número de datos es par o impar.
- 📈 El cálculo de percentiles también sigue un procedimiento similar al de los cuartiles, pero se basa en un denominador de 100.
- 🧮 Cuando se obtiene un número decimal en los cálculos, se debe interpretar como una posición entre dos datos.
- 🔍 En caso de que un número se repita, el percentil correspondiente se identifica con el número que se repite.
- 📉 Para datos no agrupados, se aplica una fórmula diferente para calcular los cuartiles y percentiles.
- 📏 Al calcular percentiles, es fundamental multiplicar el decimal obtenido por el rango entre los dos números que lo rodean.
- 👩🏫 Este proceso es aplicable tanto para cuartiles como para percentiles, manteniendo siempre el mismo procedimiento.
- 👍 Al finalizar, se recomienda compartir y suscribirse a recursos educativos para seguir aprendiendo.
Q & A
¿Qué son los cuartiles y cómo se utilizan en el análisis de datos?
-Los cuartiles son valores que dividen un conjunto de datos ordenados en cuatro partes iguales. Se utilizan para identificar la posición de ciertos valores dentro de la distribución de los datos.
¿Cuál es la importancia de organizar los datos antes de calcular cuartiles y percentiles?
-Organizar los datos es esencial porque los cuartiles y percentiles se calculan en base a la posición de los datos en un conjunto ordenado. Sin la organización adecuada, los resultados pueden ser incorrectos.
¿Cómo se calcula el tercer cuartil (Q3) para un conjunto de datos?
-Para calcular Q3, se utiliza la fórmula Q3 = (3(n + 1))/4, donde n es el número total de datos. Se encuentra la posición correspondiente y se identifica el valor en esa posición.
¿Qué fórmula se utiliza para calcular un percentil en datos no agrupados?
-La fórmula para calcular el percentil Pk es Pk = (k(n + 1))/100, donde k es el percentil deseado y n es el número total de datos.
¿Qué hacer si el resultado de la posición de un percentil es un número decimal?
-Si la posición es decimal, se debe identificar los valores en las posiciones enteras más cercanas y realizar una interpolación para encontrar el valor del percentil.
¿Qué pasos seguir para calcular el percentil 40 en un conjunto de datos?
-Primero, se organiza el conjunto de datos. Luego se calcula la posición usando la fórmula P40 = (40(n + 1))/100. Se identifica el valor correspondiente y se aplica la interpolación si la posición es decimal.
¿Cuál es la diferencia entre cuartiles y percentiles?
-Los cuartiles dividen un conjunto de datos en cuatro partes iguales, mientras que los percentiles lo dividen en 100 partes. Los cuartiles son una forma específica de percentiles.
En el ejemplo proporcionado, ¿cuál fue el valor encontrado para el cuartil 3?
-En el ejemplo, el valor encontrado para el cuartil 3 (Q3) fue 45, basado en la posición calculada en el conjunto de datos ordenados.
¿Qué procedimiento se debe seguir si se encuentra un número que se repite al calcular un percentil?
-Si se encuentra un número que se repite, como en el caso del percentil 40 que resultó ser 33, se utiliza ese valor repetido como resultado del percentil.
¿Qué se debe hacer si hay un número decimal al calcular la posición de un cuartil o percentil?
-Se deben restar los valores correspondientes a las posiciones enteras más cercanas y multiplicar el resultado por la parte decimal. Luego, se suma este resultado al valor menor.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS

CUARTILES, DECILES Y PERCENTILES PARA DATOS NO AGRUPADOS

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición
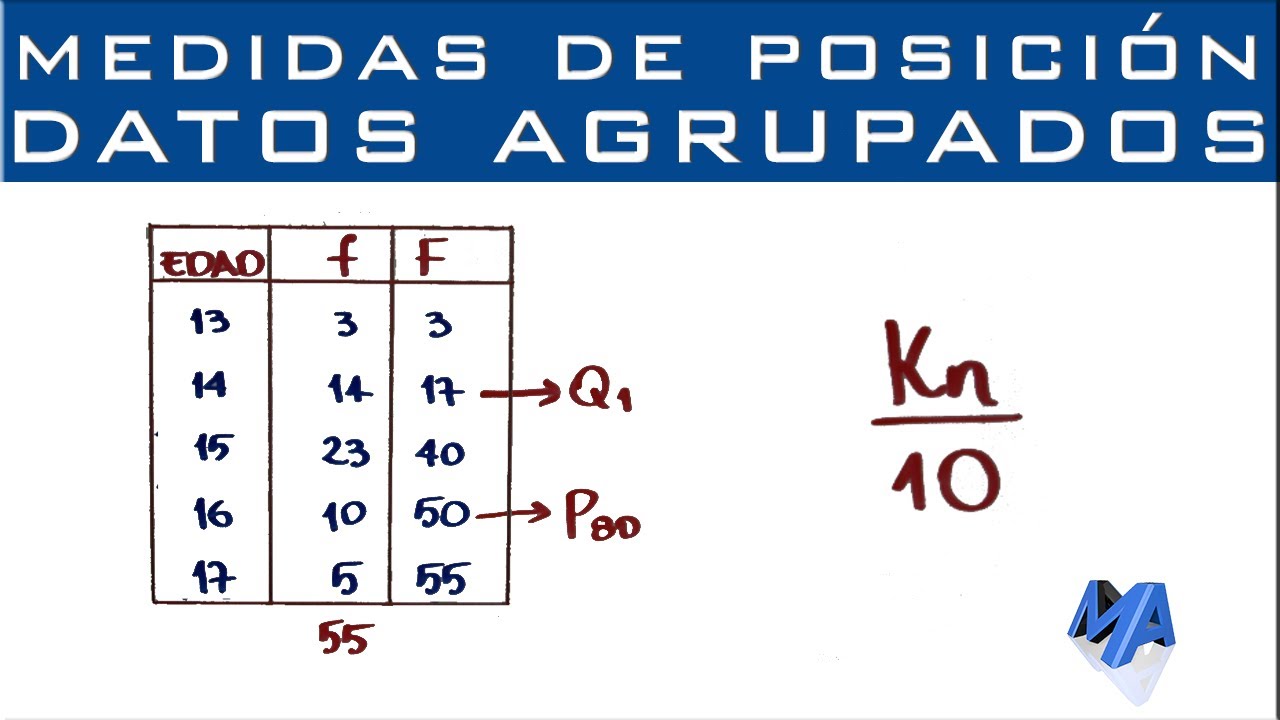
Cuartiles, Deciles y Percentiles | Datos agrupados puntualmente

Cuartiles y Rango Intercuartílico para datos agrupados en intervalos
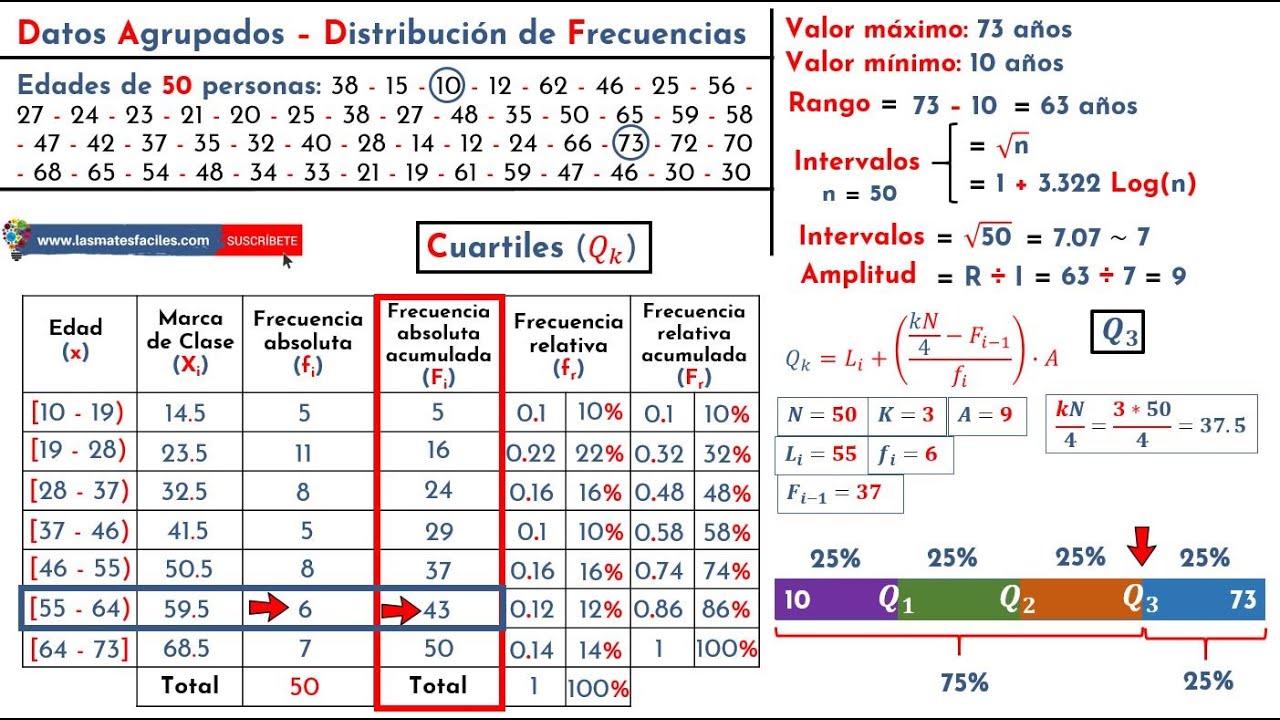
Cuartiles, Deciles y Percentiles - Datos Agrupados
5.0 / 5 (0 votes)
