Video Animasi Matematika - Fungsi Komposisi
Summary
TLDRIn this educational video, the presenter explains the concept of function composition in mathematics. Using relatable examples, such as cooking rice and making fried rice, they illustrate how various functions can be combined to create new ones. The video highlights the notation for function composition, represented as G ∘ F, and provides a step-by-step example involving specific functions. Viewers are encouraged to understand the process of substituting and manipulating functions to achieve the desired results. The video concludes with a call to action for viewers to like, comment, share, and subscribe for more informative content.
Takeaways
- 😀 The video focuses on understanding the concept of composition functions.
- 🤔 Composition functions are defined as the combination of two or more functions to create a new function.
- 🌾 An example is given involving rice, showing how it is processed from paddy to produce rice and then cooked into rice dishes.
- 👩🍳 Another example involves cooking fried rice, highlighting the ingredients like rice, onions, and eggs.
- 📚 The concept of composition functions is symbolized using notation like 'g(f(x))'.
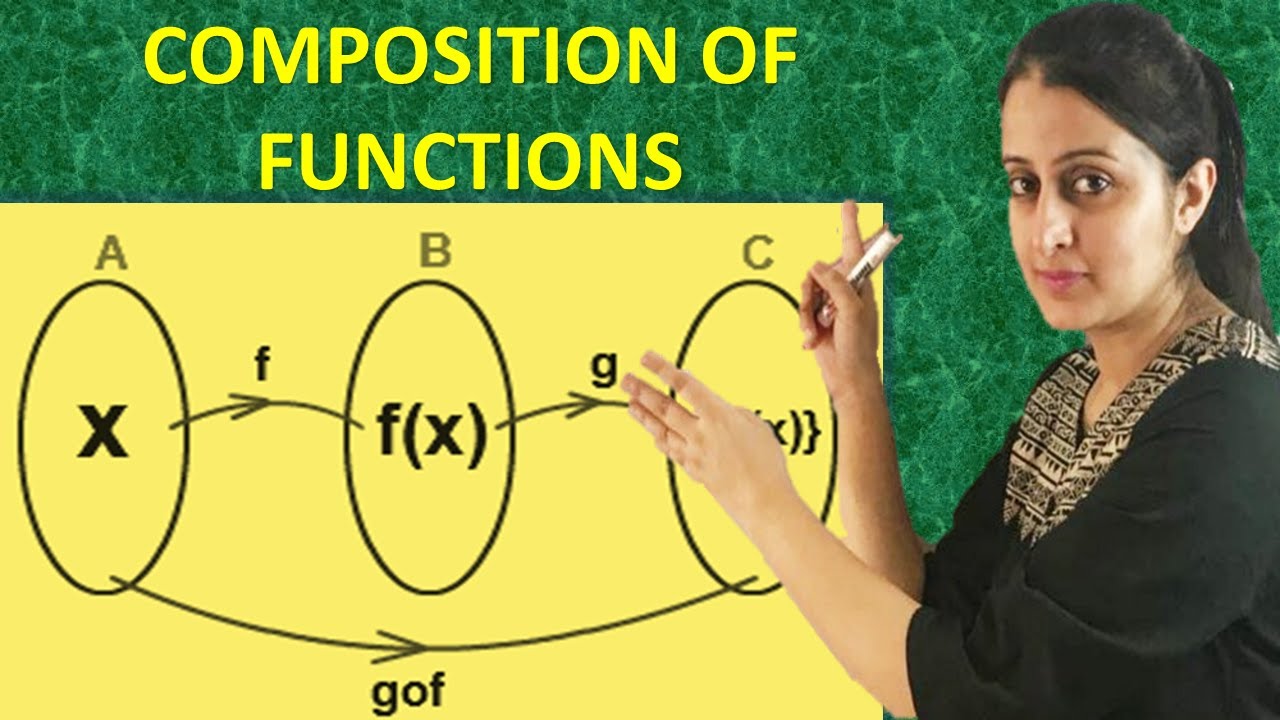
- 🔗 The relationship between sets A, B, and C is illustrated through the functions f and g.
- ✅ The composition of functions f and g can be represented as g∘f or f∘g.
- ✏️ A mathematical example is provided: if f(x) = 5x + 1 and g(x) = x + 1, then f∘g is calculated.
- 🧮 By substituting g(x) into f(x), the result simplifies to 5x + 6.
- 🙏 The video concludes with gratitude towards viewers, encouraging likes, comments, shares, and subscriptions.
Q & A
What is function composition?
-Function composition is the process of combining two or more functions to create a new function, where the output of one function becomes the input of another.
Can you provide a real-life example of function composition?
-An example is making rice from paddy. The process involves multiple steps: grinding paddy to produce rice and then cooking it to make a final dish.
What notation is commonly used to represent function composition?
-Function composition is often represented using the notation 'G ∘ F', indicating that function G is applied after function F.
How does function composition relate to sets and functions?
-In function composition, sets of inputs (domain) and outputs (codomain) are connected through functions, allowing the creation of new outputs from existing inputs.
What are the functions used in the example problem?
-The example problem uses the functions F(x) = 5x + 1 and G(x) = x + 1.
How do you calculate F(G(x))?
-To calculate F(G(x)), substitute G(x) into F(x). For example, substituting G(x) = x + 1 into F(x) gives F(G(x)) = F(x + 1) = 5(x + 1) + 1.
What is the final result of F(G(x)) for the given functions?
-The final result of F(G(x)) is 5x + 6 after substituting and simplifying.
What conclusion can be drawn about function composition from the examples provided?
-The examples demonstrate that function composition allows for complex operations by combining simpler functions, leading to a new output that reflects the combined processes.
Why is understanding function composition important in mathematics?
-Understanding function composition is important because it helps to simplify complex mathematical relationships and aids in solving problems in calculus and other areas of mathematics.
What should viewers do if they found the video helpful?
-Viewers are encouraged to like, comment, share, and subscribe to the channel for more educational content.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Pembahasan materi FUNGSI (Domain & Range, Komposisi, Invers) KELAS 10 | #MatematikAsik

Komposisi Fungsi - Matematika Wajib Kelas XI Kurikulum Merdeka

Komposisi Fungsi | XI SMA| Kurikulum Merdeka

Fungsi Komposisi dan Fungsi Invers SMA/MA/SMK

Fungsi Komposisi
CALCULUS: COMPOSITION OF FUNCTIONS (CBSE CLASS XII 12th Maths)
5.0 / 5 (0 votes)
