Probability - addition and multiplication rules
Summary
TLDRThis Tech Math video tutorial delves into calculating probabilities across multiple events, using relatable examples like flipping coins and drawing marbles. It introduces viewers to the product and addition rules in probability, explaining how to handle independent and dependent events. The video employs tree diagrams to visually map out possible outcomes and illustrates how to multiply probabilities for independent events and add them for mutually exclusive ones. It also covers scenarios with and without replacement, highlighting the impact on probability calculations. The host encourages interaction, inviting viewers to try examples and providing a call to action for likes and subscriptions.
Takeaways
- 🎓 The video discusses calculating probabilities over multiple events, such as flipping a coin multiple times or drawing marbles from a bag.
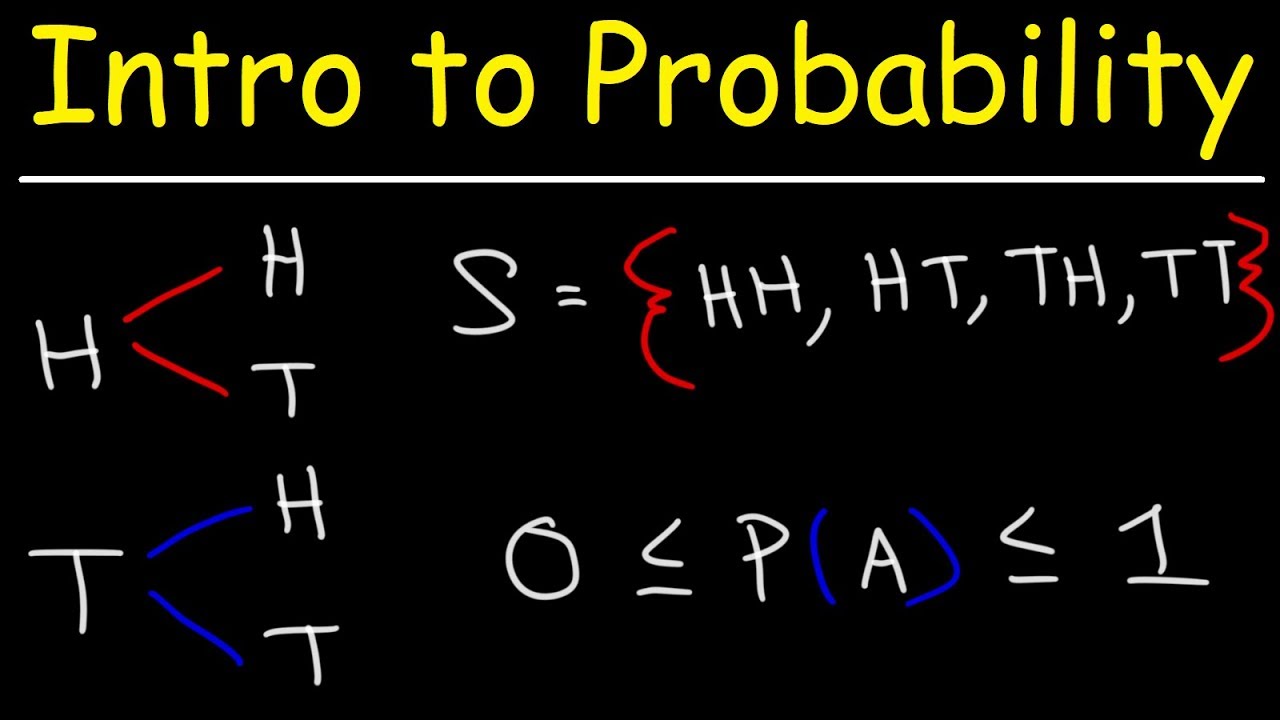
- 📊 A tree diagram is introduced as a method to visualize the different outcomes of multiple events.
- 🔄 The concept of independent events is explained, where the outcome of one event does not affect the probability of another.
- 🔗 The product rule in probability is introduced, which states that the probability of multiple independent events occurring together is found by multiplying their individual probabilities.
- 🔄 The video also covers dependent events, where the outcome of one event affects the probability of subsequent events.
- ➕ The addition rule in probability is explained, which is used to calculate the total probability of multiple mutually exclusive events occurring.
- 🎯 Examples are given to illustrate how to apply the product and addition rules in different scenarios, such as drawing marbles with and without replacement.
- 🍎 A practical example involving selecting apples from a batch with both good and bad ones is used to demonstrate the application of probability rules.
- 🧮 The importance of understanding whether events are independent or dependent is emphasized, as it affects how probabilities are calculated.
- 📈 The video encourages viewers to practice calculating probabilities by working through the examples provided.
- 👍 The presenter prompts viewers to like and subscribe for more content, and mentions the availability of merchandise and Patreon support for the channel.
Q & A
What is the main topic of the video?
-The main topic of the video is understanding how to calculate probability over multiple events, including the use of product and addition rules in probability.
What is an example used in the video to explain probability?
-An example used in the video is flipping a coin twice and calculating the probability of getting heads both times.
What is the probability of getting two heads when flipping a fair coin twice?
-The probability of getting two heads when flipping a fair coin twice is 1/4, as each flip is an independent event with a 1/2 chance of getting heads.
What is the product rule in probability as explained in the video?
-The product rule in probability states that the probability of two or more independent events occurring together is calculated by multiplying the individual probabilities of each event.
How does the video demonstrate the addition rule in probability?
-The video demonstrates the addition rule by showing that if you have two mutually exclusive events that can occur in different orders (like getting a head then a tail or a tail then a head), you add the probabilities of each sequence to find the total probability.
What is the difference between independent and dependent events as discussed in the video?
-Independent events are those where the outcome of one event does not affect the probability of the other event. Dependent events are those where the outcome of one event changes the probability of the other event.
Can you explain the marble drawing example used in the video?
-The marble drawing example involves a bag containing three blue and two red marbles. The video explains how to calculate the probability of drawing two marbles of the same color, considering both dependent (without replacement) and independent (with replacement) scenarios.
What is the significance of replacement in the context of the marble drawing example?
-Replacement signifies that after drawing a marble, it is put back into the bag, thus keeping the total number of marbles constant and making each draw independent of the others. Without replacement, the probabilities change after each draw because the total number of marbles decreases.
How does the video handle the scenario of drawing two marbles with replacement?
-In the scenario with replacement, the video shows that the probabilities remain the same for each draw because the marble is put back, making each event independent and not affected by previous draws.
What is the final example given in the video, and how does it relate to probability?
-The final example is about drawing two apples from a group of six, where three are good and three are bad. The video uses this to illustrate calculating the probabilities of drawing different combinations of good and bad apples, emphasizing the concept of dependent events.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

What are the Chances?

Materi Peluang Kelas IX SMP

Menentukan Peluang Suatu Kejadian ||Materi, Soal & Pembahasan||

Ruang Sampel dan Peluang Suatu Kejadian (Materi dan Contoh Soal diserta Pembahasan)

Probability of Independent and Dependent Events (6.2)
Introduction to Probability, Basic Overview - Sample Space, & Tree Diagrams
5.0 / 5 (0 votes)
