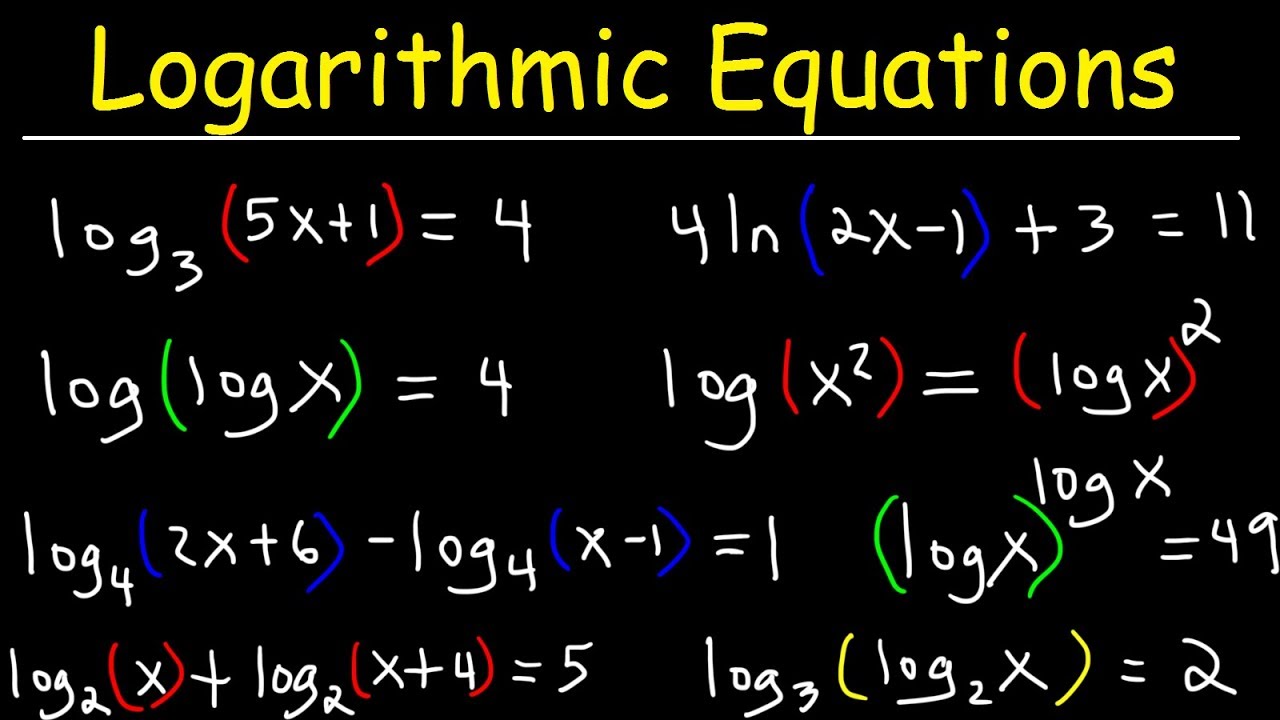Solving Exponential and Logarithmic Equations
Summary
TLDRProfessor Dave's video script is an educational guide on solving exponential and logarithmic equations. It begins with basic examples, such as 2^X = 16, and progresses to more complex scenarios like 2^X = 17, emphasizing the use of logarithms for non-intuitive solutions. The script introduces techniques like taking logarithms with different bases and applying the change-of-base formula. It also covers solving equations with compound exponents and those that cannot be simplified to a common base, using natural logarithms and algebraic manipulation. The video concludes with solving basic logarithmic equations and those requiring properties of logs, such as the product rule, to find solutions.
Takeaways
- 🔢 To solve equations like 2^X = 16, recognizing that X must be 4 is straightforward, but logarithms are necessary for less obvious numbers like 2^X = 17.
- 📚 Using logarithms, specifically log base 2, on both sides of the equation 2^X = 17 leads to X = log_2(17), providing the exact solution.
- 🧮 For a more calculator-friendly form, taking the natural log of both sides of an equation allows manipulation and solving in terms of natural logs.
- 🔑 When dealing with more complex exponents, such as 3^{2X-7} = 27, expressing both sides with the same base and then equating the exponents simplifies the solution.
- 🔄 Changing the base of an equation can alter existing exponents, as shown when converting 4^X to (2^2)^X, which simplifies to 2^{2X}.
- 📉 Logarithmic properties, like the product rule, are essential for solving equations involving multiple logs with the same base, such as log_2(X) + log_2(X-3) = 2.
- 🚫 When bases cannot be made the same, as in 3^{X+2} = 2^{X-1}, taking the natural log and manipulating the equation is necessary to solve for X.
- 🔍 Distributing the natural log over terms and rearranging them allows for factoring and solving equations with different bases on each side.
- 📐 Logarithmic equations can be solved by understanding their definitions, such as log_2(X-4) = 3 leading to X-4 = 8 and thus X = 12.
- 🔄 Applying logarithmic properties, like the product rule, to equations with multiple logs can condense them into polynomials that are easier to solve.
Q & A
What is the solution to the equation 2^X = 16?
-The solution to the equation 2^X = 16 is X = 4, as 2 raised to the power of 4 equals 16.
How can logarithms be used to solve the equation 2^X = 17?
-Logarithms can be used to solve 2^X = 17 by taking the log base 2 of both sides, which gives X = log2(17).
What is the natural log approach to solving 2^X = 17?
-By taking the natural log of both sides of the equation 2^X = 17, you get ln(2^X) = ln(17), which simplifies to X * ln(2) = ln(17). Solving for X gives X = ln(17) / ln(2).
How do you solve the equation 3^(2X - 7) = 27?
-The equation 3^(2X - 7) = 27 can be solved by recognizing that 27 is 3^3. Thus, setting the exponents equal gives 2X - 7 = 3. Solving for X results in X = 5.
What property of logarithms allows you to simplify log base two of X + log base two of (X - 3)?
-The property of logarithms that allows you to simplify log base two of X + log base two of (X - 3) is the product rule, which states that log(a) + log(b) = log(a * b).
How can you solve the equation 2^(X + 3) = 4^(X - 1)?
-The equation 2^(X + 3) = 4^(X - 1) can be solved by expressing 4 as 2^2, which gives 2^(2(X - 1)). Then, by setting the exponents equal, you get X + 3 = 2(X - 1), leading to X = 5.
What is the process for solving the equation 3^(X + 2) = 2^(X - 1) when you can't get the same base on both sides?
-For the equation 3^(X + 2) = 2^(X - 1), you take the natural log of both sides, bring the exponents to the front, distribute the log over the binomial, and then isolate terms with X on one side to solve for X.
How do you solve the logarithmic equation log2(X - 4) = 3?
-The logarithmic equation log2(X - 4) = 3 is solved by understanding that 2^3 = 8, so X - 4 must equal 8. Solving for X gives X = 12.
What is the product rule of logarithms and how is it used in the script?
-The product rule of logarithms states that log(a) + log(b) = log(a * b). In the script, it is used to combine log base two of X and log base two of (X - 3) into a single logarithm.
How can you solve a polynomial equation that results from logarithmic manipulation, as shown in the script?
-To solve a polynomial equation resulting from logarithmic manipulation, you rearrange terms to isolate the polynomial, factor if possible, and then solve for the variable.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
5.0 / 5 (0 votes)