Dominio rango y grafico función Racional | Caso 1 ejemplo 1
Summary
TLDREn este vídeo se explica cómo encontrar el dominio y el rango de una función racional, así como cómo graficarla. Se resalta la importancia de identificar los casos en que los exponentes de la 'x' en el numerador y denominador son iguales. Seguidamente, se detallan los pasos para encontrar las asíntotas verticales y horizontales, los ceros de la función y cómo utilizar esta información para graficar. El vídeo también incita a la práctica con ejercicios similares para reforzar el aprendizaje.
Takeaways
- 📚 El vídeo explica cómo encontrar el dominio y el rango de una función racional, así como cómo graficarla.
- 🔢 Se destacan tres casos importantes en función racional: exponentes iguales en numerador y denominador, exponente en numerador mayor que en denominador y viceversa.
- 📈 Se describe el proceso de graficar una función racional, incluyendo la creación de una tabla de valores y la identificación de asíntotas verticales y horizontales.
- ⚠️ Se resalta que el denominador en una función racional no puede ser cero, lo que determina la asíntota vertical.
- 📉 Las asíntotas horizontales se calculan a partir de los coeficientes principales del numerador y denominador de la función.
- 📍 Se menciona la importancia de encontrar los ceros de la función, que son puntos donde la función intersecta el eje x o el eje y.
- 📊 Se sugiere hacer una tabla de valores para localizar puntos específicos en la gráfica de la función racional.
- 💡 Se enfatiza que las asíntotas son útiles para predecir el comportamiento de la función a medida que se acerca al infinito.
- 📉 Se explica que el dominio de una función racional en este caso es todos los reales excepto el valor que hace que el denominador sea cero.
- 📊 Se aclara que el rango de la función es todos los reales excepto el valor que corresponde a la asíntota horizontal.
Q & A
¿Qué es una función racional?
-Una función racional es una que se puede expresar como la división de dos polinomios, donde tanto el numerador como el denominador son expresiones algebraicas de la variable.
¿Cuáles son los tres casos principales que se deben diferenciar en una función racional?
-Los tres casos principales son: 1) Cuando los exponentes de la x en el numerador y denominador son iguales. 2) Cuando el exponente de la x en el numerador es mayor que el del denominador. 3) Cuando el exponente de la x en el denominador es mayor que el del numerador.
¿Qué son las asíntotas y cómo se relacionan con las funciones racionales?
-Las asíntotas son líneas que el gráfico de una función tiende a acercarse, pero nunca toca. En el caso de las funciones racionales, pueden haber asíntotas verticales y horizontales que ayudan a entender el comportamiento del gráfico en puntos específicos.
¿Cómo se encuentran las asíntotas verticales en una función racional?
-Las asíntotas verticales se encuentran al determinar los valores de x que hacen que el denominador de la función sea cero, ya que no se puede dividir por cero.
¿Cómo se calcula la asíntota horizontal en una función racional?
-La asíntota horizontal se calcula tomando el coeficiente principal del numerador y dividiéndolo por el coeficiente principal del denominador, cuando los exponentes máximos de la x en ambos son iguales.
¿Qué es un cero de una función y cómo se encuentran?
-Los ceros de una función son los valores de x que hacen que el valor de la función sea cero. Se encuentran reemplazando y por 0 en la función y resolviendo la ecuación resultante.
¿Qué es el dominio de una función racional y cómo se determina?
-El dominio de una función racional es el conjunto de todos los valores de x para los cuales la función está definida. Se determina excluyendo los valores que hacen que el denominador sea cero.
¿Cómo se determina el rango de una función racional?
-El rango de una función racional es el conjunto de todos los valores que puede asumir la función. Se determina observando los valores que toma la función, especialmente en relación con las asíntotas horizontales.
¿Por qué es importante conocer las asíntotas y los ceros al graficar una función racional?
-Las asíntotas y los ceros son importantes al graficar una función racional porque proporcionan puntos de referencia clave que ayudan a entender y visualizar el comportamiento general del gráfico de la función.
¿Cómo se puede practicar para mejorar en el entendimiento de las funciones racionales y su graficado?
-Para mejorar en el entendimiento de las funciones racionales y su graficado, se recomienda pausar el video, practicar los pasos descritos, y realizar ejercicios similares para aplicar y consolidar el conocimiento.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Función inversa | Ejemplo 2

Función logarítmica Gráfica, Dominio y Rango | Ejemplo 1
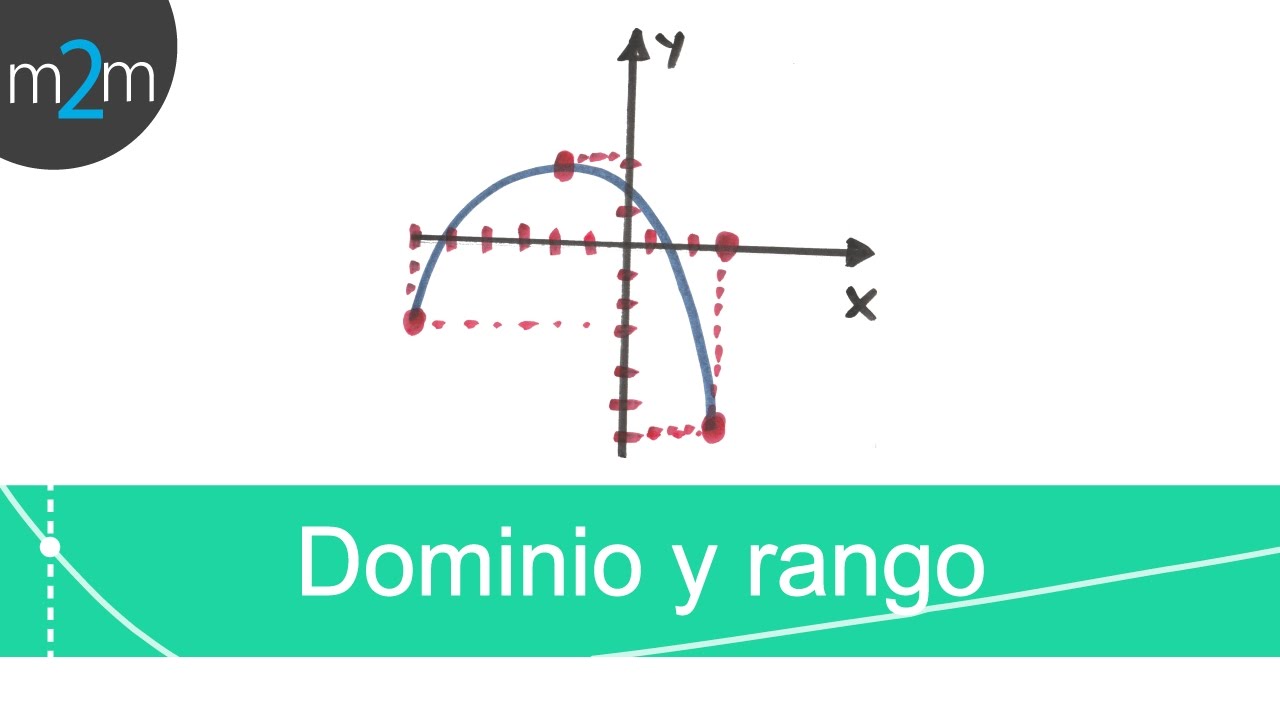
✅ Hallar el DOMINIO y RANGO de una Función a partir de su Gráfica

Función a trozos: gráfica, dominio y rango

Función Lineal (afín) - Ejercicios Resueltos - Nivel 1

▶¿Qué es una función de VARIABLE REAL ejemplos? 🌻¿Cómo identificar funciones de variable real?
5.0 / 5 (0 votes)
