Projeto e Análise de Algoritmos - Aula 12 - Algoritmos de busca em largura e profundidade em grafos
Summary
TLDRThe video script delves into the fundamentals of graph exploration through two core search algorithms: Breadth-First Search (BFS) and Depth-First Search (DFS). It explains how BFS systematically uncovers vertices at increasing distances from the starting point, using a queue to manage unexplored nodes. Conversely, DFS explores as far along a branch as possible before backtracking, utilizing recursion. The script provides a detailed walkthrough of both algorithms, including initialization, vertex marking, and the use of time stamps to track vertex discovery and completion. It also touches on the computational complexity and time consumption of these algorithms, offering insights into their practical applications.
Takeaways
- 📚 The script discusses two fundamental graph exploration algorithms: Breadth-First Search (BFS) and Depth-First Search (DFS).
- 🔍 BFS is used to systematically explore a graph from a starting vertex, discovering all vertices at the same level before moving to the next.
- 🌐 DFS, on the other hand, explores as far as possible along each branch before backtracking, creating a tree or a forest of explored vertices.
- 🔄 BFS uses a queue to keep track of vertices to explore, ensuring that vertices are processed in the order of their discovery level.
- 📈 The script explains that BFS marks vertices with different colors to indicate their state, such as unexplored, discovered, or fully explored.
- 🎯 DFS uses a stack implicitly through recursion to keep track of vertices to visit and marks them with a visit time to indicate when they were discovered.
- 🕒 Both algorithms have a time complexity of O(V + E), where V is the number of vertices and E is the number of edges in the graph.
- 📝 The script provides a step-by-step explanation of how BFS and DFS work, including the initialization process and the iterative or recursive steps involved.
- 🛠️ The pseudocode for both algorithms is presented, showing the logic behind the exploration process and the conditions checked at each step.
- 🌳 DFS can result in a spanning tree or a forest if the graph is not connected, whereas BFS will explore all vertices reachable from the starting point.
- 🔑 The script highlights the importance of these algorithms in solving various problems, such as finding paths between vertices or determining the connectivity of a graph.
Q & A
What are the two fundamental search algorithms discussed in the script?
-The two fundamental search algorithms discussed are Breadth-First Search (BFS) and Depth-First Search (DFS).
What is the primary purpose of using search algorithms in graphs?
-The primary purpose of using search algorithms in graphs is to explore or traverse the graph systematically, which is essential for solving various problems such as finding paths between vertices.
How does Breadth-First Search (BFS) explore a graph?
-BFS explores a graph by visiting all the vertices at the present depth before going deeper to the vertices at the next depth level. It uses a queue to keep track of the vertices to be explored.
What does the term 'level' refer to in the context of BFS?
-In the context of BFS, 'level' refers to the shortest distance from the source vertex to the current vertex, measured in the number of edges.
How does Depth-First Search (DFS) differ from Breadth-First Search (BFS) in terms of exploration strategy?
-DFS differs from BFS in that it explores as far as possible along a branch before backtracking. It uses a stack (either explicitly or via recursion) to remember where to continue the search.
What is the significance of marking vertices in search algorithms?
-Marking vertices is significant to keep track of which vertices have been visited to avoid revisiting them and to prevent infinite loops in the search process.
What data structure is typically used to implement the queue in BFS?
-A queue data structure is typically used to implement BFS, where vertices are dequeued in the order they were enqueued, ensuring exploration by levels.
How does the script describe the process of updating distances in BFS?
-The script describes the process of updating distances in BFS by stating that when a vertex is dequeued, its adjacent vertices are examined, and their distances are updated if they are further from the source vertex than the current vertex.
What is the purpose of the 'predecessor' concept in DFS?
-The 'predecessor' concept in DFS is used to keep track of how the algorithm arrived at each vertex, which is essential for reconstructing paths or understanding the order of exploration.
How does the script explain the time complexity of BFS and DFS in terms of operations on a queue or stack?
-The script explains that each vertex and edge is enqueued and dequeued once in BFS, and similarly, each vertex is pushed and popped once in DFS, leading to a time complexity of O(V + E) for both algorithms, where V is the number of vertices and E is the number of edges.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Breadth First Search BFS
AI - Ch03 - Uninformed search algorithms
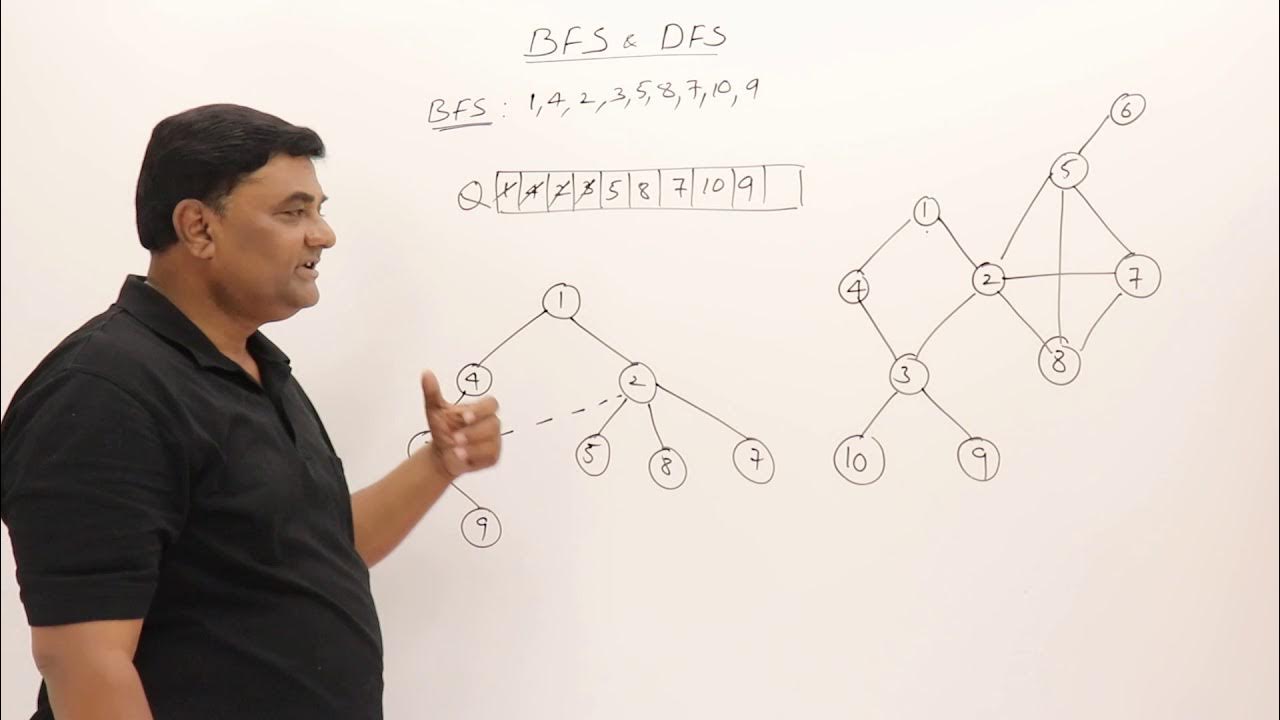
5.1 Graph Traversals - BFS & DFS -Breadth First Search and Depth First Search

Algoritma Greedy Best First Search dan A* (A star) + Contoh dan Penjelasan | Algoritma Struktur Data

Depth First Search (DFS) Graph Traversal in Data Structures
The Best Order to learn Algorithms & Data Structures?
5.0 / 5 (0 votes)
