Movimento Harmônico Simples - Aula 02 (Força no MHS)
Summary
TLDRThe video script is an educational lecture on simple harmonic motion (SHM), focusing on the mathematical representation of oscillatory motion using sine and cosine functions. It explains the restoring force in SHM, which is proportional to the displacement from equilibrium and is described by Hooke's law (F = -kx). The lecture further delves into the concepts of force, acceleration, and velocity in the context of SHM, highlighting their relationships and behavior at various points in the motion cycle. It also clarifies misconceptions about the forces and accelerations at the extremes and at the equilibrium point of SHM, using examples and emphasizing the symmetry of the motion.
Takeaways
- 📚 The script is a lecture about simple harmonic motion (SHM), focusing on the mathematical representation using sine and cosine functions.
- 🔍 It explains that SHM can be described by oscillatory and periodic functions, which are harmonic functions in mathematics.
- 📐 The lecture uses the spring-mass system as an example to illustrate the principles of SHM, where the mass is attached to a spring.
- 🔄 The force acting on the mass in SHM is variable and depends on the displacement from the equilibrium position, calculated as \( F = -kx \) where \( k \) is the spring constant and \( x \) is the displacement.
- 🚫 The force in SHM is a restoring force, which acts to bring the system back to its equilibrium position, always pointing towards the center of the trajectory.
- ➡️ The force in SHM has a maximum magnitude at the extremes (amplitude) and is zero at the equilibrium position.
- 🔢 The lecture emphasizes the importance of understanding the algebraic sign of the force, which can be positive or negative depending on the direction of displacement.
- 📉 The acceleration in SHM is also variable and is directly related to the force, increasing as the force increases and decreasing as the force decreases, following Newton's second law.
- 🔄 The acceleration has a maximum magnitude at the extremes of the motion and is zero at the equilibrium position, opposite in direction to the velocity at those points.
- 📈 The script discusses the symmetry of the SHM, where the behavior on one side of the equilibrium position is a mirror image of the other.
- 📚 Finally, the lecture provides examples and exercises to help students understand the concepts of force, acceleration, and velocity in SHM, including the calculation of spring constant.
Q & A
What is a simple harmonic motion (SHM)?
-Simple harmonic motion is a type of periodic motion where an object moves back and forth over the same path within a stabilizing force proportional to the displacement from an equilibrium position, often described by sine or cosine functions.
What are the restoring forces in SHM?
-The restoring forces in SHM are proportional to the displacement from the equilibrium position and act in the opposite direction to bring the object back to its equilibrium state.
How is the force in SHM calculated?
-The force in SHM is calculated using the formula F = -kx, where F is the restoring force, k is the spring constant, and x is the displacement from the equilibrium position.
What is the relationship between force and displacement in SHM?
-In SHM, the force is directly proportional to the displacement from the equilibrium position, with the force being maximum at the extremes of displacement and zero at the equilibrium point.
What is the difference between the algebraic value and the magnitude of the force in SHM?
-The algebraic value of the force can be positive or negative depending on the direction of the displacement, while the magnitude of the force is always positive and represents the strength of the force regardless of direction.
How does the acceleration in SHM relate to the force?
-According to Newton's second law, the acceleration in SHM is directly proportional to the force acting on the object. As the force increases or decreases, the acceleration does the same.
What is the amplitude of SHM?
-The amplitude of SHM is the maximum displacement of the object from its equilibrium position, representing the extent of the motion.
What is the frequency of SHM and how is it related to the period?
-The frequency of SHM is the number of oscillations per unit time and is the inverse of the period. The period is the time taken for one complete oscillation, and the frequency is the reciprocal of the period.
At what points is the velocity of an object in SHM zero?
-The velocity of an object in SHM is zero at the points of maximum displacement, which are the equilibrium position's extremes.
What is the acceleration of an object at the equilibrium position in SHM?
-At the equilibrium position in SHM, where the displacement is zero, the acceleration is also zero because the restoring force, and hence the acceleration, is proportional to the displacement.
How does the direction of acceleration in SHM compare to the direction of velocity?
-In SHM, the direction of acceleration is opposite to the direction of velocity. When the object moves away from the equilibrium position, the acceleration is directed towards it, and vice versa.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Persamaan Gerak Harmonik | Gerak Osilasi | Part 1 | Fisika Dasar
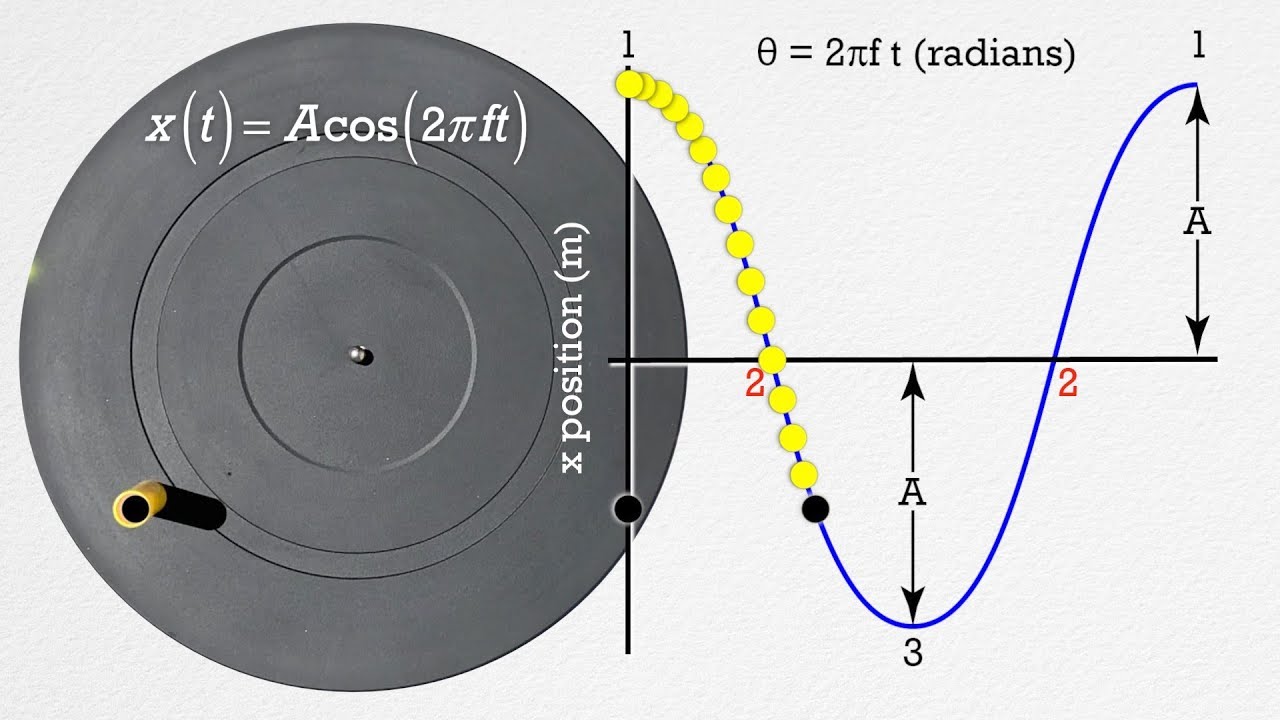
Simple Harmonic Motion(SHM) - Position Equation Derivation

Getaran dan Gerak Harmonik Sederhana: Definisi, Titik Seimbang, Simpangan, Amplitudo, dan Periode

Comparing Simple Harmonic Motion(SHM) to Circular Motion - Demonstration

Simple Harmonic Motion & Damped Motion | lect.-01 | Classical Mechanics #physics #bsc

Fisika SMA - Gerak Harmonik (1) - Pengenalan Gerak Harmonik Sederhana, Periode dan Frekuensi (I)
5.0 / 5 (0 votes)
