S1.5.1 and S1.5.2 Ideal gases and deviation from ideal gas behaviour

Summary

This video explores the deviation of real gases from ideal gas behavior. Ideal gases, as per kinetic molecular theory, have no volume, no intermolecular forces, and their kinetic energy is directly proportional to temperature. Real gases, however, exhibit deviations, especially at low temperatures and high pressures, due to finite volume and intermolecular forces. The video illustrates these concepts with graphs and examples, highlighting how gases like hydrogen and nitrogen show less deviation than those with stronger intermolecular forces, such as carbon dioxide and methane. It concludes with a comparison between ideal and real gases, noting that real gases follow the Van der Waals equation rather than the simple ideal gas law.

Takeaways

• 🌟 Ideal gases are hypothetical and follow the gas laws and kinetic molecular theory, with no intermolecular forces and negligible volume.
• 🌡 Real gases deviate from ideal behavior due to finite volume and intermolecular forces, especially at low temperatures and high pressures.
• 📊 At standard conditions, real gases' molar volumes are similar to the ideal gas value of 22.414 cubic decimeters per mole, indicating near-ideal behavior.
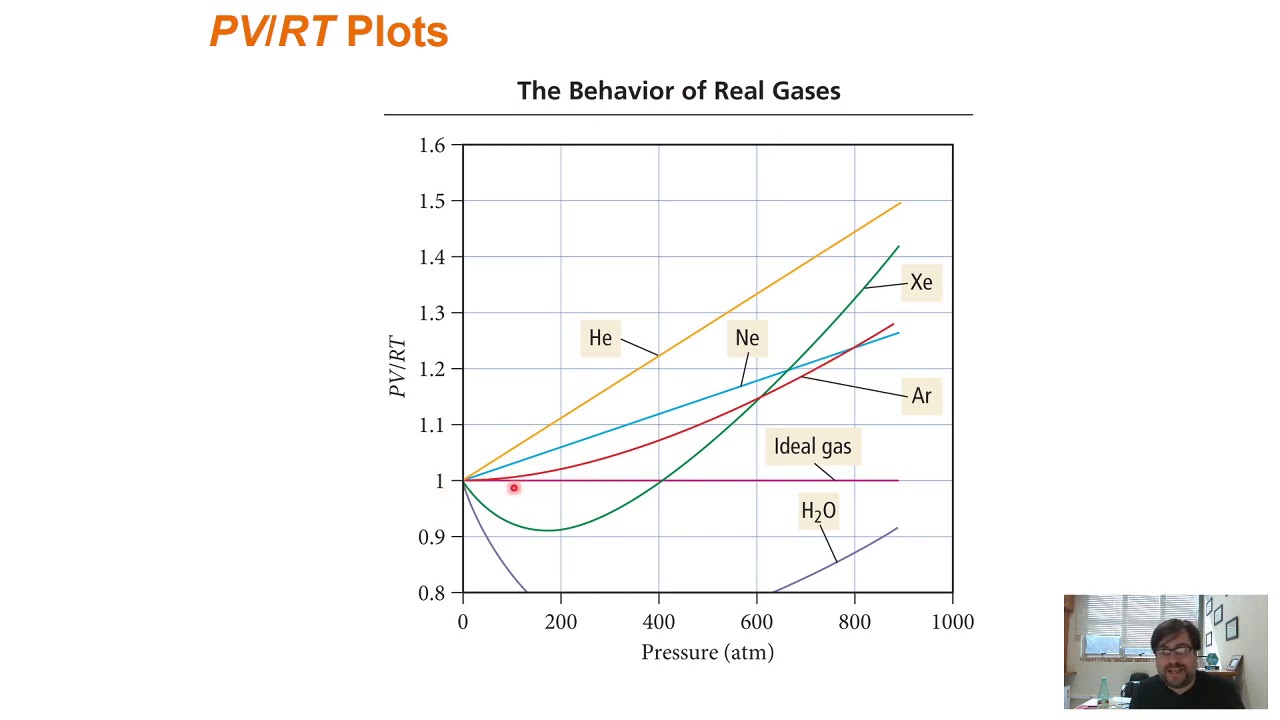
• 📉 The deviation of real gases from ideal behavior increases at low temperatures and high pressures, as shown by the graph comparing pv/rt ratios.
• ⚖️ The ideal gas law, pv = nrt, is rearranged to solve for moles, n, and is always equal to one for ideal gases, but not for real gases.
• 🔍 At moderately high pressures, real gases show deviation from ideal behavior due to intermolecular forces reducing the effective pressure.
• 🔍 At very high pressures, the deviation is due to the molecular volume becoming significant compared to the container volume, increasing the pv/rt ratio.
• 🚀 At higher temperatures, gases behave more ideally as particles have enough kinetic energy to overcome intermolecular forces.
• 🌌 Different gases show varying degrees of deviation from ideal behavior, influenced by the strength of their intermolecular forces.
• 🏷 Gases with weaker intermolecular forces, like hydrogen, show less deviation from ideal gas behavior compared to those with stronger forces, like carbon dioxide and methane.
• 🔄 Real gases are described by the van der Waals equation, which accounts for molecular volume and intermolecular forces, unlike the ideal gas law.

Q & A

What is an ideal gas according to the kinetic molecular theory?

An ideal gas is a hypothetical gas that obeys the gas laws and kinetic molecular theory, characterized by particles in constant random straight-line motion, elastic collisions, negligible volume compared to the container, no intermolecular forces, and average kinetic energy directly proportional to the absolute temperature in Kelvin.

How does a real gas differ from an ideal gas?

A real gas deviates from ideal gas behavior by having a finite, measurable volume, intermolecular forces acting between particles, and exhibiting deviations from ideal behavior especially at low temperatures and high pressures.

What is the molar volume of an ideal gas at standard temperature and pressure (STP)?

The molar volume of an ideal gas at STP is 22.414 cubic decimeters per mole.

Under what conditions do real gases behave almost ideally?

Real gases behave almost ideally under conditions of relatively high temperatures and low pressures.

What does the product of PV over RT represent in the context of ideal gases?

For an ideal gas, the product of PV over RT is always equal to one, which is derived from the ideal gas equation rearranged to solve for the amount in moles (n).

How does the deviation of real gases from ideal behavior manifest at different temperatures and pressures?

Real gases deviate the most from ideal behavior at low temperatures and high pressures. At moderately high pressures, the product PV/RT is less than one due to intermolecular forces, and at very high pressures, it is greater than one due to the effects of molecular volume.

What causes the deviation from ideal gas behavior at moderately high pressures?

At moderately high pressures, the deviation from ideal gas behavior is mainly because of the effects of intermolecular forces, which reduce the force of collisions with the container wall, resulting in a lower pressure and thus a PV/RT value less than one.

What is the reason for the deviation from ideal behavior at very high pressures?

At very high pressures, the deviation from ideal behavior is mainly because of the effects of molecular volume. As the external pressure increases, the volume occupied by the gas particles becomes significant, reducing the available volume for the gas particles and thus increasing the PV/RT value above one.

How does temperature affect the deviation of a real gas from ideal gas behavior?

At lower temperatures, the particles in a real gas have lower average kinetic energy and are less able to overcome intermolecular forces, showing greater deviation from ideal behavior. As temperature increases, real gases behave more ideally due to the particles having sufficient kinetic energy to overcome these forces.

Why do gases with stronger intermolecular forces show more deviation from ideal gas behavior at moderately high pressures?

Gases with stronger intermolecular forces, such as carbon dioxide and methane, show more deviation from ideal behavior at moderately high pressures because these forces have a more significant impact on the gas particles' motion and collision with the container walls.

What is the fundamental difference between the behavior of ideal gases and real gases in terms of intermolecular forces and volume?

Ideal gases are assumed to have no intermolecular forces and their volume is considered negligible. In contrast, real gases have intermolecular forces acting between particles and occupy a finite, measurable volume.

What equation describes the behavior of real gases, as opposed to the ideal gas law?

Real gases obey the van der Waals equation, which accounts for the effects of molecular volume and intermolecular forces, unlike the ideal gas law (PV=nRT) which assumes ideal behavior.