Data Representation - Mantissa And Exponents Part 3 - (A Level Computer Science Made Easy (A2) )
Summary
TLDRIn this video, the concept of mantissa and exponents in floating point representation is explained. The video covers how to express real numbers in exponential form using binary, including the conversion of positive and negative numbers. The process involves shifting binary points, using two's complement, and understanding the balance between mantissa accuracy and exponent range. Additionally, the video touches on normalization and demonstrates examples of converting mantissa and exponents into decimal form, offering a clear understanding of this complex topic.
Takeaways
- 📚 Mantissa and exponents are part of the floating-point representation used to express real numbers in exponential form.
- 🔢 The number 1978.381 can be represented in floating-point as 0.1987381 * 10^4.
- 🌐 In scientific notation, numbers are typically expressed as ±M * R^E, where M is the mantissa, R is the base, and E is the exponent.
- 💡 The base for decimal floating-point numbers is 10, while for binary floating-point it is 2.
- 🛠 Mantissa and exponents are often represented in two's complement form, which involves flipping bits and adding one.
- 🔍 Increasing the number of bits for the mantissa improves the accuracy of the number, while more bits for the exponent increase the range of expressible numbers.
- 👉 The conversion of positive numbers to mantissa and exponents involves separating the integer and fractional parts, converting them to binary, and then combining them with a sign bit.
- 🔄 For negative numbers, the process involves using 2's complement, which includes flipping bits and adding one to the binary representation.
- 📉 Normalization ensures more bits are assigned to the mantissa for accuracy, requiring the most significant bit and the one after it to be different.
- 🚀 There are limits to the largest and smallest numbers that can be represented in floating-point, which are subject to overflow and underflow errors.
- 🔑 Understanding the process of converting from mantissa and exponents to decimal numbers involves flipping bits for negative values, adding one to get two's complement, and then shifting the binary point by the exponent value.
Q & A
What is the purpose of mantissa and exponents in floating point representation?
-Mantissa and exponents are used in floating point representation to express real numbers in exponential form, allowing for efficient storage and manipulation of a wide range of numerical values.
How is the number 1978.381 represented in exponential form?
-The number 1978.381 can be represented in exponential form as 0.1987381 multiplied by 10 raised to the power of 4.
What is the significance of the base number in mantissa and exponents representation?
-The base number, commonly 10 in decimal systems and 2 in binary systems, is the base to which the exponent is applied in the exponential form of a number.
What does it mean when the number of bits for the mantissa is increased?
-Increasing the number of bits for the mantissa increases the accuracy of the number by allowing more precise representation of the fractional part.
How does increasing the number of bits for the exponent affect the representation?
-Increasing the number of bits for the exponent increases the range of numbers that can be expressed, allowing for both larger and smaller numbers to be represented.
Can you provide an example of converting a positive number to mantissa and exponents?
-Yes, the number 8.75 can be converted to mantissa and exponents by separating it into 8 and 0.75, converting each part to binary, and then combining them with an appropriate exponent.
What is the process for converting a negative number to mantissa and exponents?
-To convert a negative number, you split the number at the decimal point, convert each part to binary, use 2's complement for the significant digits, and then combine them with the appropriate exponent.
What is normalization in the context of mantissa and exponents?
-Normalization ensures that the most significant bit of the mantissa is always 1 (except for the special case of zero), which allows for more bits to be assigned to the mantissa, improving accuracy.
Why is it important to know the largest and smallest numbers representable in floating point?
-Knowing the largest and smallest representable numbers helps in understanding the limitations of the floating point representation and avoiding overflow or underflow errors.
How does the script demonstrate converting mantissa and exponents from binary to decimal?
-The script provides step-by-step examples of converting binary representations of mantissa and exponents, including the use of 2's complement for negative numbers, to their decimal equivalents.
What is the significance of the most significant bit in determining the sign of a number in binary representation?
-The most significant bit indicates the sign of a number in binary representation; a 0 indicates a positive number, while a 1 indicates a negative number, affecting the process of converting to decimal.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
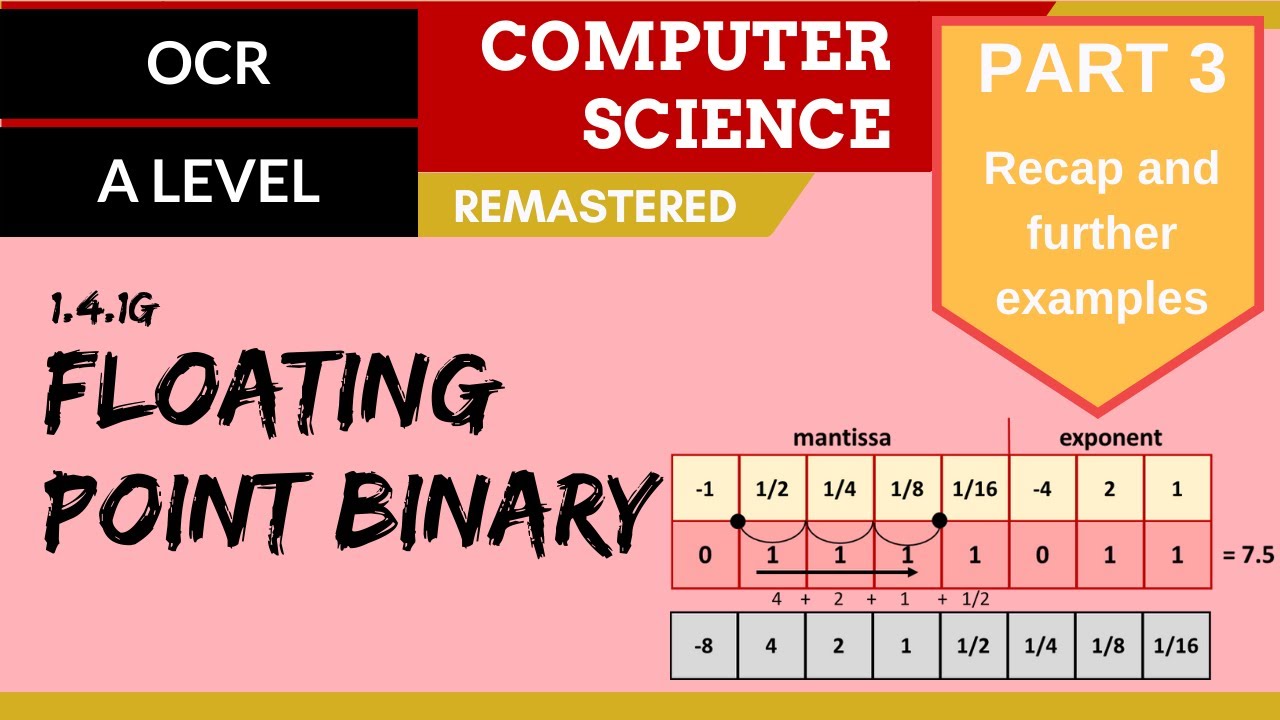
81. OCR A Level (H446) SLR13 - 1.4 Floating point binary part 3 - Recap and further examples

ECAP268 - U01L04 - Fixed point and floating point representation

79. OCR A Level (H046-H446) SLR13 - 1.4 Floating point binary part 1 - Overview

Floating Point Numbers: IEEE 754 Standard | Single Precision and Double Precision Format

HOW TO: Convert Decimal to IEEE-754 Single-Precision Binary

80. OCR A Level (H046-H446) SLR13 - 1.4 Floating point binary part 2 - Normalisation
5.0 / 5 (0 votes)
