Hidden Markov Model Clearly Explained! Part - 5

Summary

In this 'Normalized Nerd' video, the presenter delves into Hidden Markov Models (HMMs), a concept derived from Markov chains, which are widely used in fields like bioinformatics and natural language processing. The video offers both intuition and mathematical insights into HMMs, illustrating their workings with a hypothetical scenario involving weather and mood. It explains the model's components, including the transition and emission matrices, and demonstrates how to calculate the probability of a sequence of observed variables. The presenter also introduces the use of Bayes' theorem in determining the most likely sequence of hidden states, providing a clear and engaging explanation of the complex topic.

Takeaways

• 😀 Hidden Markov Models (HMMs) are an extension of Markov chains and are used in various fields such as bioinformatics, natural language processing, and speech recognition.
• 🔍 The video aims to explain both the intuition and the mathematics behind HMMs, including the role of Bayes' theorem in the process.
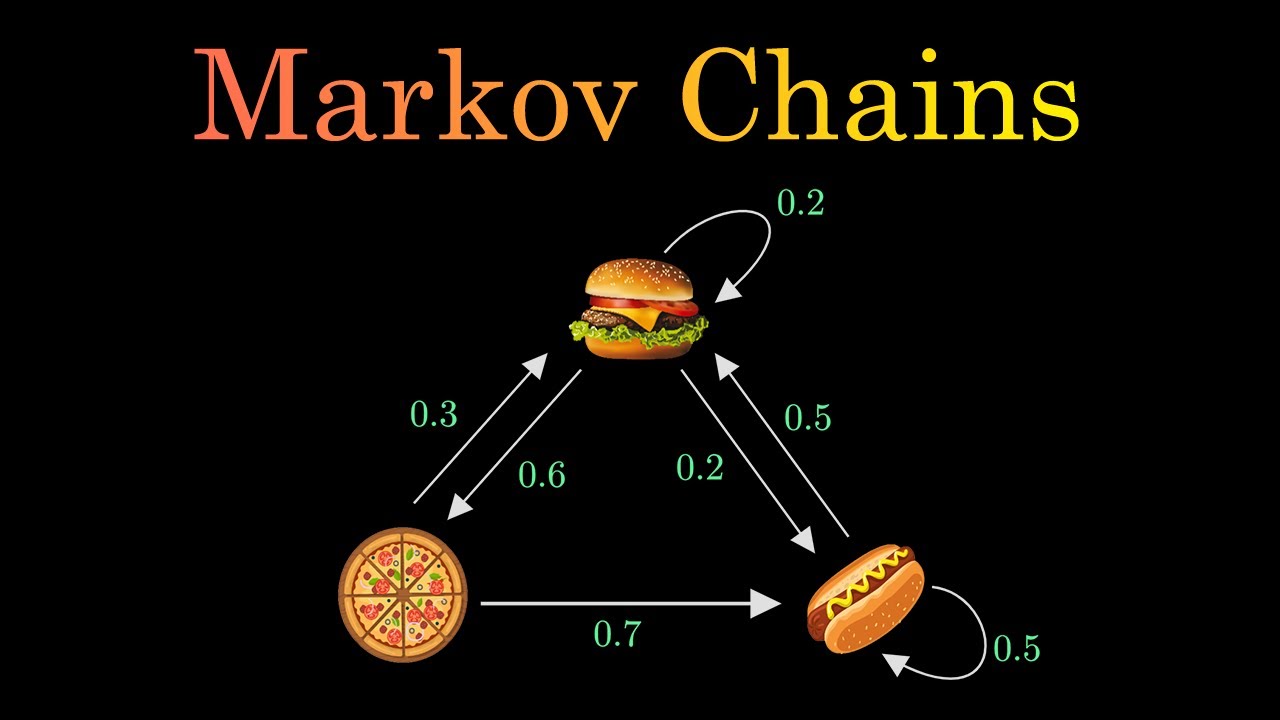
• 🌤️ The script uses a hypothetical town with three types of weather (rainy, cloudy, sunny) to illustrate the concept of a Markov chain where the weather tomorrow depends only on today's weather.
• 🤔 It introduces the concept of 'hidden' states by showing that while we can't observe the weather directly, we can infer it from Jack's mood, which is an observed variable dependent on the weather.
• 📊 The script explains the use of matrices to represent the probabilities of state transitions (transition matrix) and the probabilities of observed variables given the states (emission matrix).
• 📚 It emphasizes the importance of understanding the basics of Markov chains before diving into HMMs, suggesting viewers watch previous videos for a foundation.
• 🧩 The video provides a step-by-step example of calculating the joint probability of an observed mood sequence and a hypothetical weather sequence using the Markov property and matrices.
• 🔑 The concept of the stationary distribution of a Markov chain is introduced as necessary for calculating the probability of the initial state in the HMM.
• 🔍 The video poses the question of finding the most likely sequence of hidden states given an observed sequence, a common problem in applications of HMMs.
• 📈 The script explains the formal mathematical approach to solving HMM problems using Bayes' theorem and the joint probability distribution of hidden and observed variables.
• 📝 The video concludes by encouraging viewers to rewatch if they didn't understand everything, highlighting the complexity of the topic and the elegance of the mathematical solution.

Q & A

What is the main topic discussed in the video?

The main topic discussed in the video is Hidden Markov Models (HMMs), their concept, intuition, and mathematics, with applications in bioinformatics, natural language processing, and speech recognition.

What is the relationship between Hidden Markov Models and Markov Chains?

Hidden Markov Models are derived from Markov Chains. They consist of an ordinary Markov Chain and a set of observed variables, where the states of the Markov Chain are unknown or hidden, but some variables dependent on the states can be observed.

Why is the concept of 'emission matrix' important in HMMs?

The 'emission matrix' in HMMs captures the probabilities corresponding to the observed variables, which depend only on the current state of the Markov Chain. It's essential for understanding the relationship between the hidden states and the observable outcomes.

What is the role of Bayes' Theorem in Hidden Markov Models?

Bayes' Theorem is used in HMMs to find the most likely sequence of hidden states given a sequence of observed variables. It helps in rewriting the problem of finding the probability of hidden states given observed variables into a more manageable form.

How does the video script illustrate the concept of Hidden Markov Models using Jack's hypothetical town?

The script uses Jack's town, where the weather (rainy, cloudy, sunny) and Jack's mood (sad, happy) are the variables. The weather is the hidden state, and Jack's mood is the observed variable. The script explains how these variables interact and how HMMs can be used to predict the weather based on Jack's mood.

What is the significance of the 'transition matrix' in the context of the video?

The 'transition matrix' represents the probabilities of transitioning from one state to another in the Markov Chain. In the video, it shows how the weather changes from one day to the next, which is essential for modeling the sequence of states in HMMs.

What is the purpose of the 'stationary distribution' in calculating the probability of the first state in HMMs?

The 'stationary distribution' is used to find the probability of the initial state in a Markov Chain. It is necessary because the probability of the first state cannot be directly observed and must be inferred from the long-term behavior of the system.

How does the video script explain the computation of the probability of a given scenario in HMMs?

The script explains the computation by breaking down the scenario into a product of terms from the emission matrix and transition matrix, and using the stationary distribution for the initial state probability. It provides a step-by-step approach to calculate the joint probability of the observed mood sequence and the weather sequence.

What is the most likely weather sequence for a given mood sequence according to the video?

The video does not provide the specific sequence but explains the process of finding the most likely weather sequence for a given mood sequence by computing the probability for each possible permutation and selecting the one with the maximum probability.

How does the video script help in understanding the formal mathematics behind HMMs?

The script introduces symbols to represent the hidden states and observed variables, explains the use of Bayes' Theorem, and simplifies the problem into a form that can be maximized. It provides a clear explanation of the mathematical expressions involved in HMMs, making the formal mathematics more accessible.