Gauss's Law Basics
Summary
TLDRThe video discusses a common mistake regarding electric fields. It clarifies that the electric field is actually parallel to the differential area element (dA), not perpendicular as often assumed. This distinction is important in understanding the correct application of Gauss’s Law in physics, particularly when dealing with flux and field lines. The clarification helps viewers grasp key concepts in electromagnetism more effectively.
Takeaways
- 😀 The electric field is parallel to the differential area element (dA), not perpendicular.
- 😀 The error in the original statement was the assumption of the electric field's direction relative to dA.
- 😀 Understanding the relationship between the electric field and dA is crucial in calculating flux.
- 😀 The concept of electric flux is influenced by the orientation of the electric field and the surface it interacts with.
- 😀 The correction emphasizes the importance of correctly identifying the electric field's direction when applying Gauss's Law.
- 😀 Accurate representation of the electric field's relationship with the surface area ensures proper application of physical principles.
- 😀 Electric flux is calculated by considering the dot product of the electric field vector and the area vector.
- 😀 The angle between the electric field and the surface area vector directly affects the magnitude of the flux.
- 😀 Misunderstanding the direction of the electric field can lead to incorrect calculations of flux or field strength.
- 😀 Ensuring the correct orientation of vectors in flux calculations is essential for accurate results in electromagnetism.
Q & A
What is the key mistake mentioned in the transcript?
-The mistake is that the electric field is actually parallel to the differential area element (dA) and not perpendicular as was previously stated.
Why is the direction of the electric field important in this context?
-The direction of the electric field relative to dA is crucial because it determines the flux calculation in electrostatics. The flux is influenced by how the electric field aligns with the surface element.
What is meant by 'dA' in the transcript?
-In the context of electromagnetism, 'dA' refers to a differential area element, which represents an infinitesimally small portion of a surface.
What is the significance of the electric field being parallel to dA?
-When the electric field is parallel to dA, it means that the electric field is oriented along the surface element, which affects how the flux through the surface is calculated.
How does the incorrect assumption about the electric field's direction impact calculations?
-If the electric field is incorrectly assumed to be perpendicular to dA, the flux calculation will be inaccurate, leading to incorrect results in determining the electric field or charge distribution.
What is the correct relationship between the electric field and the differential area element?
-The correct relationship is that the electric field should be parallel to the differential area element (dA) in order to correctly calculate the flux. The flux is maximized when the electric field and dA are aligned.
What concept is being addressed in this transcript regarding the electric field?
-The concept being addressed is electric flux, specifically how the direction of the electric field relative to the surface affects the calculation of the flux through that surface.
Why is the electric field typically assumed to be perpendicular to surfaces in many problems?
-In many problems, the electric field is assumed to be perpendicular to surfaces for simplicity, as this assumption often leads to more straightforward calculations, particularly when using Gauss's law.
What might be the consequences of not understanding the correct relationship between the electric field and dA?
-Not understanding this relationship can lead to errors in calculating the electric flux, which is fundamental to solving problems involving electric fields and charges in electrostatics.
How can this mistake in the direction of the electric field be corrected in future calculations?
-To correct this mistake, one should carefully consider the orientation of the electric field relative to the surface element and ensure it is aligned with dA when performing flux calculations.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Medan, Beda Potensial dan Energi Listrik

Campo elétrico: Tudo que você precisa saber sobre um dos campos mais importantes da Física

Partikel A dan B masing-masing bermuatan +8 mu C dan +18 mu C. Titik C terletak di antara partike...

OSI Model Explained | OSI Animation | Open System Interconnection Model | OSI 7 layers | TechTerms
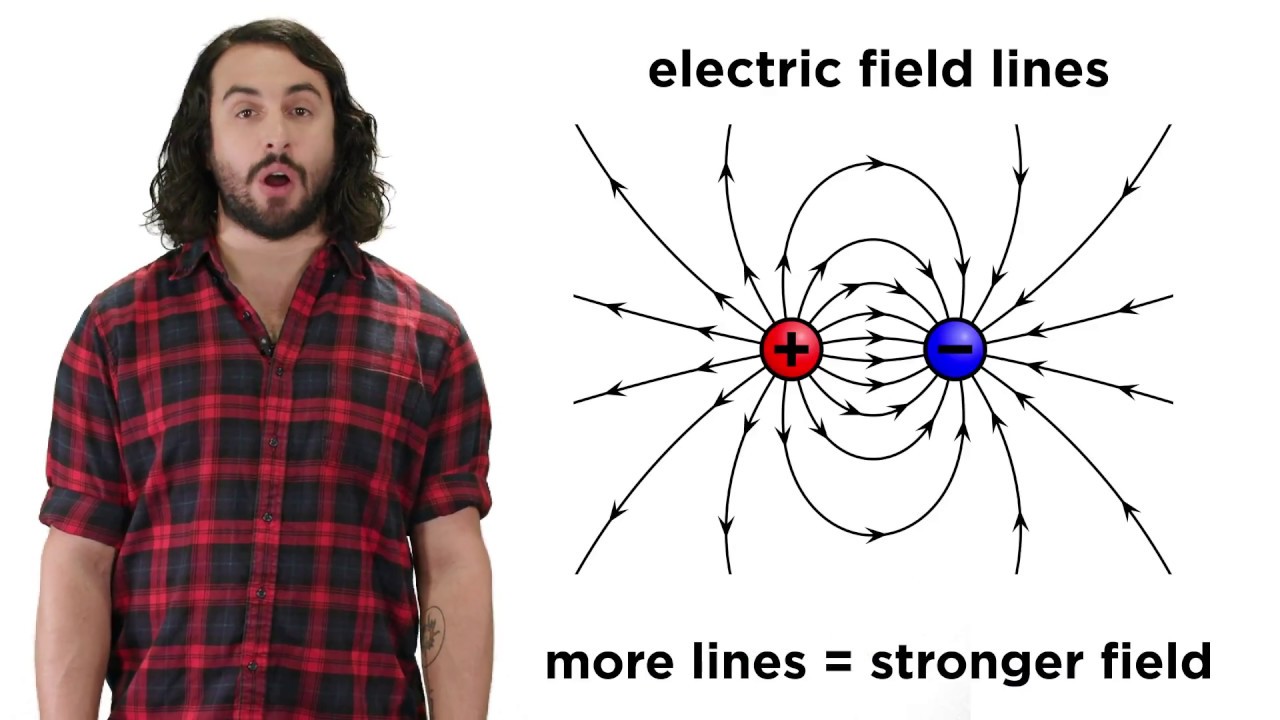
Electric Charge and Electric Fields

¿Qué es el electromagnetismo? | 101 Videos
5.0 / 5 (0 votes)
