TRIGONOMETRI (Konversi Koordinat Kutub Ke Koordinat Kartesius)
Summary
TLDRThis educational video explains the process of converting polar coordinates to Cartesian coordinates using an example. The polar coordinates (r = 20, θ = 120°) are given, and the video demonstrates step-by-step how to calculate the corresponding Cartesian coordinates (x, y) using trigonometric functions. The explanation covers the formulas for x = r * cos(θ) and y = r * sin(θ), showing the calculations and the reasoning behind each step. The final result is Cartesian coordinates (-10, 10√3), with an emphasis on understanding the relationship between angles and trigonometric values in different quadrants.
Takeaways
- 😀 The script explains how to convert polar coordinates to Cartesian coordinates.
- 😀 The given polar coordinates in the example are 20, 120°, where 20 is the radius (r) and 120° is the angle (θ).
- 😀 Cartesian coordinates are represented as (x, y), and the goal is to find the values of x and y.
- 😀 To calculate x, the formula used is x = r * cos(θ).
- 😀 For θ = 120°, since it is not a standard angle in trigonometric tables, the cosine value is calculated using the relationship with 180°.
- 😀 The angle 120° is in the second quadrant, and thus cos(120°) is negative.
- 😀 cos(60°) is used to compute cos(120°), and the result is -1/2.
- 😀 The value of x is calculated as x = 20 * (-1/2), which equals -10.
- 😀 To calculate y, the formula used is y = r * sin(θ).
- 😀 For θ = 120°, sin(120°) is positive in the second quadrant, and sin(60°) is used for the calculation.
- 😀 The value of sin(60°) is √3/2, so y = 20 * (√3/2), which simplifies to 10√3.
Q & A
What are polar coordinates?
-Polar coordinates are a system of coordinates used to specify the position of a point in a plane by using a radius (r) and an angle (θ). The radius is the distance from the origin, and the angle is the direction from the origin in terms of a standard reference angle.
What does the script explain in terms of converting polar coordinates to Cartesian coordinates?
-The script explains the process of converting polar coordinates to Cartesian coordinates by using the formulas x = r * cos(θ) and y = r * sin(θ).
What is the given polar coordinate in the script?
-The given polar coordinate in the script is (r = 20, θ = 120°).
How is the x-coordinate calculated in the conversion?
-To calculate the x-coordinate, the formula x = r * cos(θ) is used. For θ = 120°, it is necessary to first calculate cos(120°), which equals -1/2. Then, x = 20 * (-1/2) = -10.
Why is cos(120°) negative?
-Cos(120°) is negative because 120° lies in the second quadrant of the unit circle, where cosine values are negative.
How is the y-coordinate calculated in the conversion?
-To calculate the y-coordinate, the formula y = r * sin(θ) is used. For θ = 120°, it is necessary to first calculate sin(120°), which equals √3/2. Then, y = 20 * (√3/2) = 10√3.
What quadrant is the angle of 120° located in, and how does this affect the signs of trigonometric functions?
-The angle of 120° is located in the second quadrant, where cosine is negative and sine is positive. This affects the signs of the trigonometric functions when calculating the x and y coordinates.
What is the final Cartesian coordinate after conversion?
-The final Cartesian coordinate after the conversion is (-10, 10√3).
Why is it important to understand the quadrant when converting polar to Cartesian coordinates?
-Understanding the quadrant is important because it helps determine the correct signs for the trigonometric functions, which are essential in accurately calculating the Cartesian coordinates.
What mathematical identity is used to simplify the calculation of sine and cosine values for 120°?
-The script uses the identity cos(180° - 60°) and sin(180° - 60°) to simplify the calculation of cos(120°) and sin(120°), where 120° is expressed in terms of 60° to use known values from trigonometric tables.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Konversi Koordinat Cartesius ke Koordinat Kutub/ Polar dan Sebaliknya

Coordenadas Polares ¿Qué son? EXPLICACIÓN COMPLETA

CARA MENGUBAH KOORDINAT DMS KE DD
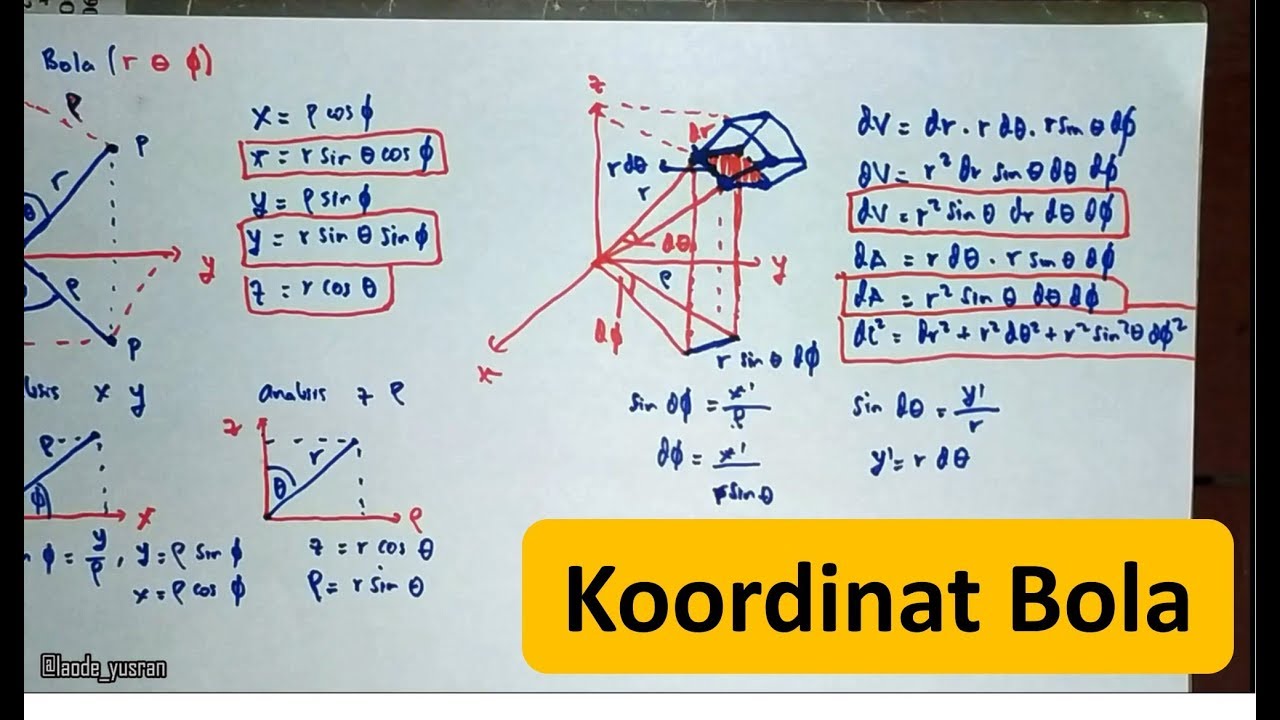
Fisika Matematika : Sistem Koordinat Bola

Vector Algebra (LEC -33) Polar coordinate system || Polar coordinate system || in Hindi ||

Matematika SMA - Trigonometri (6) - Koordinat Polar, Koordinat Kutub dan Kartesius (A)
5.0 / 5 (0 votes)
