Introdução à elipse
Summary
TLDRThis video lesson explains the concept of an ellipse, its importance in fields like physics, optics, and astronomy. The instructor describes the geometry of an ellipse, using a string-and-pin model to demonstrate its key properties, such as the major and minor axes, foci, and eccentricity. The lesson covers how the shape of the ellipse changes based on the relationship between its axes, and its relevance in celestial orbits, particularly in astronomy. The lesson concludes with an example calculation and equation of an ellipse, providing a solid foundation for further exploration of the topic.
Takeaways
- 😀 An ellipse is a shape that appears in various fields like physics, optics, and astronomy.
- 😀 The ellipse has two important foci, which are fundamental to its geometry.
- 😀 A string tied at both foci and used to trace the ellipse demonstrates the relationship between the foci and the shape.
- 😀 The total length of the string is always constant and equal to the major axis of the ellipse.
- 😀 The major axis of an ellipse is the longest diameter, while the minor axis is the shortest diameter.
- 😀 The focal distance (c) is the distance from the center of the ellipse to each focus.
- 😀 The equation for an ellipse involves the relationship between the semi-major axis (a), semi-minor axis (b), and focal distance (c).
- 😀 The excentricity of an ellipse is always less than 1, and it describes how stretched the ellipse is.
- 😀 As the excentricity approaches zero, the ellipse becomes more circular, and the foci coincide.
- 😀 In astronomy, the orbits of celestial bodies, like planets, are elliptical in nature around the sun.
- 😀 The equation for an ellipse is often written as x²/a² + y²/b² = 1, where a is the semi-major axis and b is the semi-minor axis.
- 😀 The script also explains how to calculate the equation for an ellipse when given specific parameters, like the center and foci positions.
Q & A
What is an ellipse, and how is it defined?
-An ellipse is a geometric figure that looks like a flattened circle. It is defined by two focal points, and all points on the ellipse maintain a constant sum of distances to these two foci.
What is the importance of the two foci in an ellipse?
-The two foci are crucial in defining the ellipse. They help in determining the geometric shape by ensuring that for any point on the ellipse, the sum of the distances to these foci is constant.
How can an ellipse be drawn using a string method?
-To draw an ellipse, fix a string (representing the constant sum of distances) between the two foci, and use it to trace the shape by moving the string and ensuring the total length from any point on the ellipse to the two foci remains constant.
What are the semi-major and semi-minor axes of an ellipse?
-The semi-major axis (denoted as 'a') is the longest distance from the center to the edge of the ellipse, while the semi-minor axis (denoted as 'b') is the shortest distance from the center to the edge.
What does the 'eccentricity' of an ellipse represent?
-The eccentricity of an ellipse represents how stretched or elongated it is. It is calculated using the formula where the distance between the foci divided by the semi-major axis (c/a) must be less than 1, indicating that the ellipse is not a perfect circle.
What happens to an ellipse as its eccentricity approaches 0?
-As the eccentricity approaches 0, the ellipse becomes more circular. This means that the foci get closer together, and the shape becomes less elongated.
How does the eccentricity relate to the orbits in astronomy?
-In astronomy, the orbits of celestial bodies, like planets around the Sun, are elliptical. The degree of their eccentricity determines how elongated or circular their orbits are, influencing their motion and the distance from the Sun.
What is the relationship between the axes and the equation of an ellipse?
-The equation of an ellipse is expressed as (x^2/a^2) + (y^2/b^2) = 1, where 'a' is the length of the semi-major axis and 'b' is the length of the semi-minor axis. This equation describes the shape and size of the ellipse in a coordinate plane.
In the given example, what is the value of 'a' and how is it determined?
-In the given example, 'a' (the semi-major axis) is 5, as it is stated that the ellipse has a semi-major axis equal to 5. This value defines the longest radius of the ellipse.
What does the equation of the ellipse look like when the semi-major axis is 5 and the semi-minor axis is 3?
-The equation of the ellipse in this case would be (x^2/25) + (y^2/9) = 1, where 25 is the square of the semi-major axis (5^2), and 9 is the square of the semi-minor axis (3^2).
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
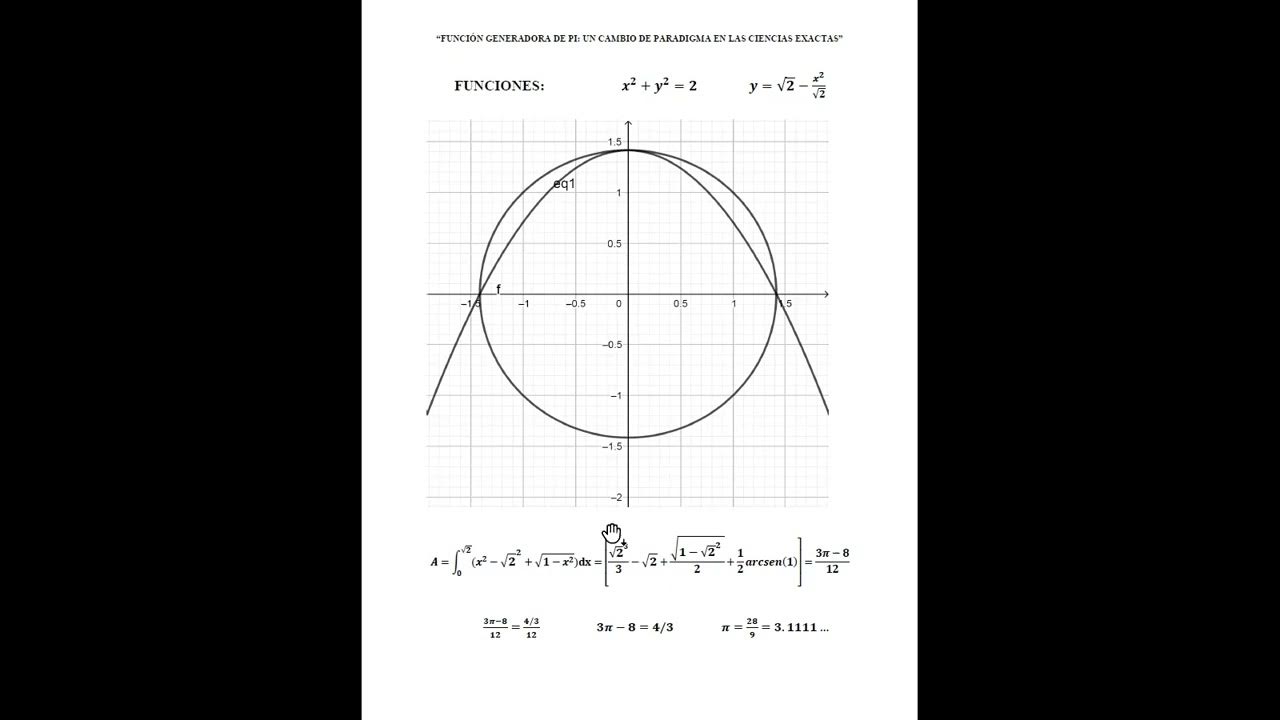
LA FUNCION M FUNCION GENERADORA DE π

Superposition principle || 3D animated explanation || class12th physics || Electric charges & fields

Ramos da física - Física

APRENDA FUNÇÕES DE UMA VEZ POR TODAS: Como resolver Funções | Resumo de Matemática para o Enem

1001 Inventions and The Library of Secrets -Sub. Indonesia HD

REFLEXÃO TOTAL DA LUZ - ÓPTICA - Aula 9 - Prof. Boaro
5.0 / 5 (0 votes)
