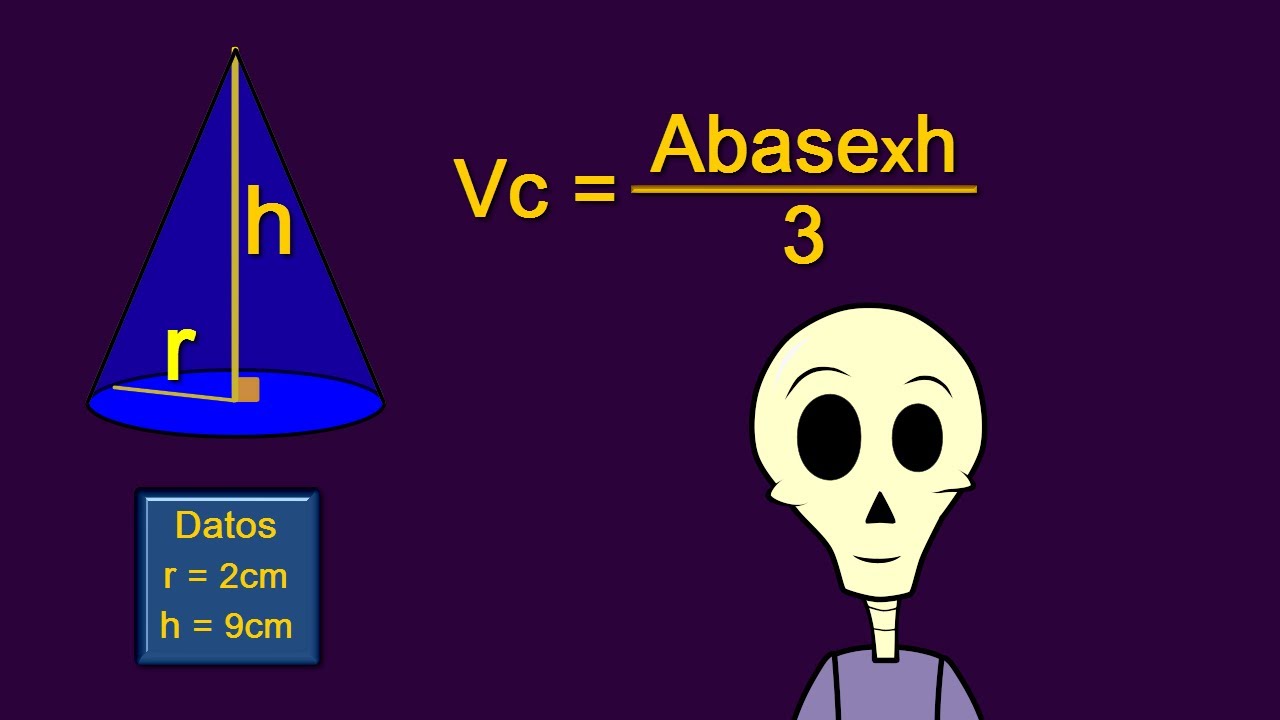
Relación de volumen entre el cilindro y el cono

Ana María Pertupe Vásquez

22 Dec 201703:11

Summary

TLDREn este video, se demuestra que la capacidad de un cono es la tercera parte de la de un cilindro, siempre que ambos tengan la misma base y altura. El proceso comienza con la construcción de los desarrollos planos del cono y el cilindro, seguidos de su armado. Posteriormente, se realiza una demostración física usando azúcar, demostrando cómo el volumen del cono cabe tres veces en el volumen del cilindro. Finalmente, se realiza una demostración analítica, donde se calcula el volumen de ambos sólidos y se confirma que el volumen del cono es efectivamente un tercio del cilindro.

Takeaways

😀 Se demuestra que la capacidad de un cono es la tercera parte de la capacidad de un cilindro con la misma base y altura.
😀 Los materiales necesarios para la demostración incluyen desarrollos planos, tijeras, y hojas para las mediciones.
😀 Es importante que el cono y el cilindro tengan la misma base y altura al realizar la demostración física.
😀 Se utiliza azúcar como material para la demostración física del volumen del cono y cilindro.
😀 Se realiza una medición del volumen del cilindro, obteniendo un resultado de 356.37 cm³.
😀 Para el cono, la fórmula del volumen es la misma que la del cilindro, pero dividida entre 3.
😀 Después de realizar las mediciones del cono, el volumen obtenido es de 118.79 cm³.
😀 Se demuestra de manera física que el volumen del cono es un tercio del volumen del cilindro.
😀 La fórmula matemática del volumen del cilindro es pi por radio al cuadrado por altura.
😀 La demostración analítica confirma que la capacidad del cono es un tercio de la capacidad del cilindro.

Q & A

¿Qué es lo que se busca demostrar en este contenido?
-El objetivo es demostrar que la capacidad de un cono es la tercera parte de la capacidad de un cilindro, siempre y cuando ambos tengan la misma base y la misma altura.
¿Cuáles son los materiales necesarios para realizar la demostración?
-Los materiales necesarios incluyen un cono y un cilindro, tijeras para recortar, azúcar (o material similar) para la demostración física, y hojas para los desarrollos planos de las figuras.
¿Qué es un desarrollo plano en este contexto?
-Un desarrollo plano es la representación bidimensional de una figura tridimensional, como un cono o cilindro, que se recorta y arma para crear las figuras en 3D.
¿Cómo se realiza la demostración física de la relación entre los volúmenes?
-Para la demostración física, se llena el cilindro con azúcar y luego se transfiere al cono. Se observa que el cono solo puede contener un tercio de la cantidad de azúcar que el cilindro, demostrando así que el volumen del cono es un tercio del volumen del cilindro.
¿Qué fórmula se utiliza para calcular el volumen de un cilindro?
-La fórmula para calcular el volumen de un cilindro es V = π * r² * h, donde r es el radio de la base y h es la altura.
¿Qué fórmula se utiliza para calcular el volumen de un cono?
-La fórmula para calcular el volumen de un cono es V = (1/3) * π * r² * h, lo que muestra que el volumen del cono es un tercio del volumen del cilindro con la misma base y altura.
¿Qué volumen se obtiene al calcular el volumen del cilindro en el ejemplo?
-El volumen del cilindro calculado en el ejemplo es de 356.37 centímetros cúbicos.
¿Qué volumen se obtiene al calcular el volumen del cono en el ejemplo?
-El volumen del cono calculado en el ejemplo es de 118.79 centímetros cúbicos.
¿Cómo se relacionan los volúmenes del cono y el cilindro según los cálculos?
-Según los cálculos, el volumen del cono es un tercio del volumen del cilindro, ya que el volumen del cono es 118.79 cm³, mientras que el del cilindro es 356.37 cm³.
¿Por qué es importante que el cono y el cilindro tengan la misma base y la misma altura en este experimento?
-Es crucial que el cono y el cilindro tengan la misma base y altura para que la comparación entre sus volúmenes sea válida. De lo contrario, los volúmenes no serían directamente comparables.