Conjuntos Numéricos: Números Racionais (Aula 2 de 4)

Summary

This lesson introduces the set of rational numbers, emphasizing that fractions are ratios of two integers with a non-zero denominator. It explains how integers and natural numbers are subsets of rational numbers. The lesson covers the concept of decimals resulting from fractions, differentiating between exact decimals and repeating decimals (periodic decimals). The process of determining whether a fraction leads to an exact or periodic decimal by factoring the denominator is also explained. The lesson concludes by addressing irrational numbers like square roots, showing that even between two rationals, there are gaps in the number line, which irrational numbers fill.

Takeaways

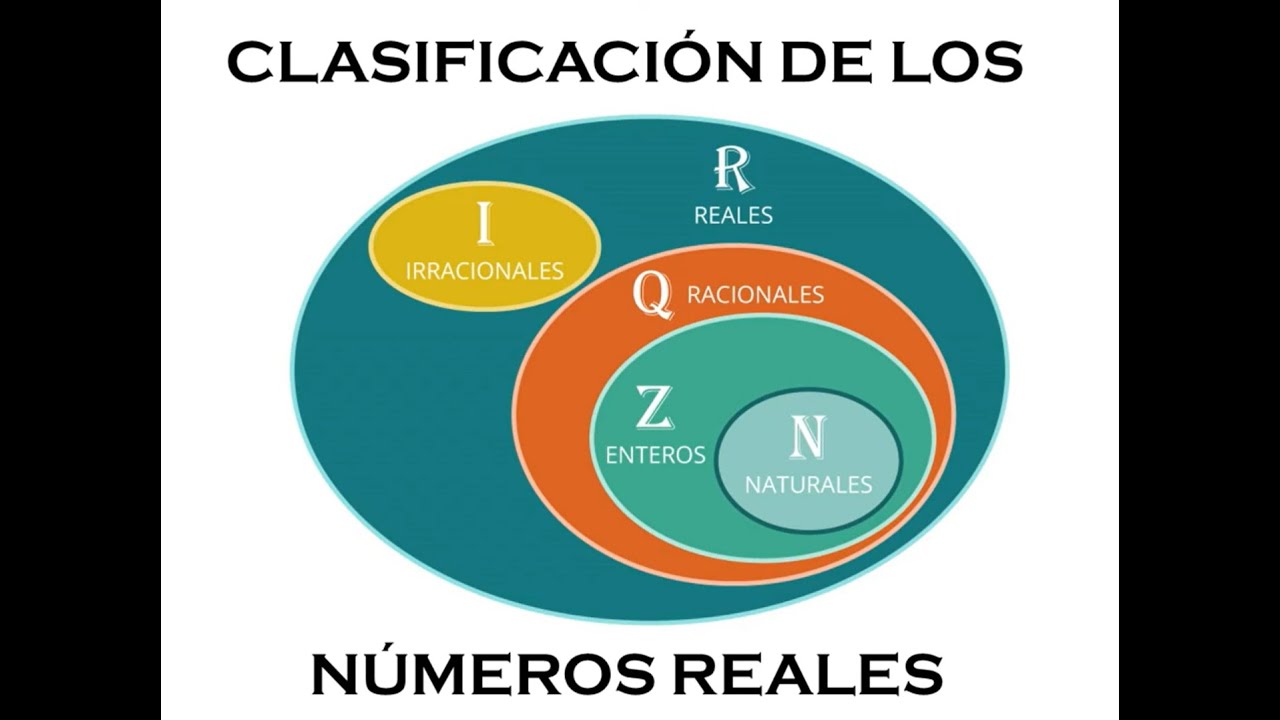
• 😀 The natural numbers (N) start from 0 or 1 and include all positive whole numbers.
• 😀 Integers (Z) extend natural numbers to include negative whole numbers and zero.
• 😀 Division in the integer set doesn't always result in another integer (e.g., 3 ÷ 2).
• 😀 Rational numbers (Q) are fractions where both the numerator and denominator are integers, and the denominator cannot be zero.
• 😀 Natural numbers and integers are subsets of rational numbers, meaning they are contained within the rational number set.
• 😀 Fractions can result in either integers or decimals when simplified or divided.
• 😀 Decimals can either be exact (e.g., 0.4) or repeating (e.g., 0.3333...), depending on the fraction.
• 😀 A fraction results in an exact decimal if the denominator only has 2 and 5 as prime factors (e.g., 7/50).
• 😀 A fraction results in a repeating decimal if the denominator has any prime factor other than 2 or 5 (e.g., 16/30).
• 😀 Between any two rational numbers, there are infinitely many other rational numbers, illustrating the density of rational numbers.
• 😀 Irrational numbers (like √2 and π) cannot be expressed as fractions and do not fit into the rational number set, filling gaps on the number line.

Q & A

What is the set of rational numbers?

The set of rational numbers is the set of fractions or quotients formed by dividing two integers, where the denominator is not zero. This set is represented by the symbol 'Q'.

What is the difference between integers and rational numbers?

Integers are whole numbers that can be positive, negative, or zero, and they do not always result in integers when divided. Rational numbers, on the other hand, are fractions formed by the division of two integers, and they can result in either whole numbers, exact decimals, or repeating decimals.

Can natural numbers be considered rational numbers?

Yes, natural numbers can be considered rational numbers because they can be represented as fractions with a denominator of 1, for example, 2/1, 3/1, etc.

What are the two types of decimal results when dividing rational numbers?

When dividing rational numbers, the result can either be an exact decimal (for example, 0.4) or a repeating decimal (such as 0.3333..., which is a periodic decimal).

How can you distinguish between an exact decimal and a repeating decimal?

An exact decimal has a finite number of decimal places (for example, 0.4), while a repeating decimal continues infinitely in a repeating pattern (such as 0.3333... or 0.7777...).

What is the rule for determining whether a fraction is an exact decimal or a repeating decimal?

A fraction will result in an exact decimal if the denominator has only 2 and/or 5 as its prime factors. If there are other prime factors in the denominator, the fraction will result in a repeating decimal.

How can we determine whether 7/50 results in an exact or repeating decimal?

To check, decompose the denominator 50 into its prime factors (2 and 5). Since the factors are only 2 and 5, the result will be an exact decimal, which is 0.14.

How can we determine whether 16/30 results in an exact or repeating decimal?

When decomposing the denominator 30, we find a factor of 3 (in addition to 2 and 5), which indicates that the result will be a repeating decimal. Dividing 16 by 30 gives 0.53333..., which repeats.

What is the significance of the rational numbers being 'dense' on the number line?

Rational numbers are dense on the number line, meaning that between any two rational numbers, you can always find another rational number. For example, the average of 1/3 and 1/2 is 5/12, which is another rational number between them.

Why are irrational numbers such as √2 and π not considered rational numbers?

Irrational numbers like √2 and π cannot be expressed as fractions of integers, and their decimal expansions do not terminate or repeat. They occupy spaces on the number line between rational numbers but cannot be represented as rational numbers.