Pembahasan Soal OSN K SMA 2024 No. 1 - Olimpiade Matematika SMA Tingkat Kabupaten Kota
Summary
TLDRThe transcript explains a mathematical problem where the perimeter of two rectangles is given as 60. The task is to calculate the area of a square based on the relationship between its side length and the dimensions of the rectangles. By simplifying the perimeter equations and solving for the side length, it is determined that the side length of the square (P) is 10. Consequently, the area of the square is calculated as 100 square units.
Takeaways
- 😀 The problem involves a square that is divided into two rectangles.
- 😀 The sum of the perimeters of the two rectangles equals 60.
- 😀 The dimensions of the square are represented by 'p' for length and 'p' for width.
- 😀 The lengths of the rectangles are denoted by 'P' and 'B', and the widths are denoted by 'X' and 'Y'.
- 😀 The perimeter of a rectangle is calculated as 2 times the length plus 2 times the width.
- 😀 The perimeter equation is 2P + 2Y + 2B + 2X = 60.
- 😀 After simplifying, the equation becomes 4P + 2Y + 2X = 60.
- 😀 It is identified that X + Y equals P.
- 😀 Substituting this relationship leads to the equation 6P = 60.
- 😀 Solving for P gives P = 10, which represents the length of the square.
- 😀 The area of the square is calculated as P * P, which equals 100.
Q & A
What is the initial problem presented in the transcript?
-The problem involves a square divided into two rectangles, and the sum of the perimeters of these rectangles equals 60. The goal is to calculate the area of the square.
How are the dimensions of the square and rectangles labeled?
-The side of the square is labeled as 'p', and the dimensions of the two rectangles are labeled as 'x' and 'y'. The side lengths of the square and the dimensions of the rectangles are related.
What formula is used to calculate the perimeter of a rectangle?
-The perimeter of a rectangle is calculated using the formula: 2 * (length + width). In this case, the first rectangle has a perimeter of 2 * (p + y), and the second rectangle has a perimeter of 2 * (b + x).
What equation is derived from the sum of the perimeters of the two rectangles?
-The sum of the perimeters is 60, leading to the equation: 2(p + y) + 2(b + x) = 60.
How is the equation simplified?
-The equation simplifies to: 4p + 2y + 2x = 60.
What relationship between the variables x, y, and p is given in the transcript?
-It is given that x + y = p, meaning the sum of the dimensions x and y equals the side length p of the square.
What happens after substituting the relation x + y = p into the equation?
-After substituting x + y = p into the equation 4p + 2y + 2x = 60, the equation becomes 6p = 60.
What is the value of p after solving the equation 6p = 60?
-Solving 6p = 60 gives p = 10.
How is the area of the square calculated?
-The area of the square is calculated by squaring the side length p. Since p = 10, the area is 10 * 10 = 100.
What is the final result of the problem?
-The final result is that the area of the square is 100 square units.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Perimeter and area: the basics | Perimeter, area, and volume | Geometry | Khan Academy

Areas & Perimeter of Rectangles and Rectilinear Shapes

Membuat Model Matematika Sistem Persamaan Linear Dua Variabel

ÁREA E PERÍMETRO | RESOLUÇÃO DE PROBLEMAS | EXERCÍCIOS

KELILING DAN LUAS PERSEGI - SEGITIGA DAN SEGIEMPAT (12) - MATEMATIKA SMP KELAS 7
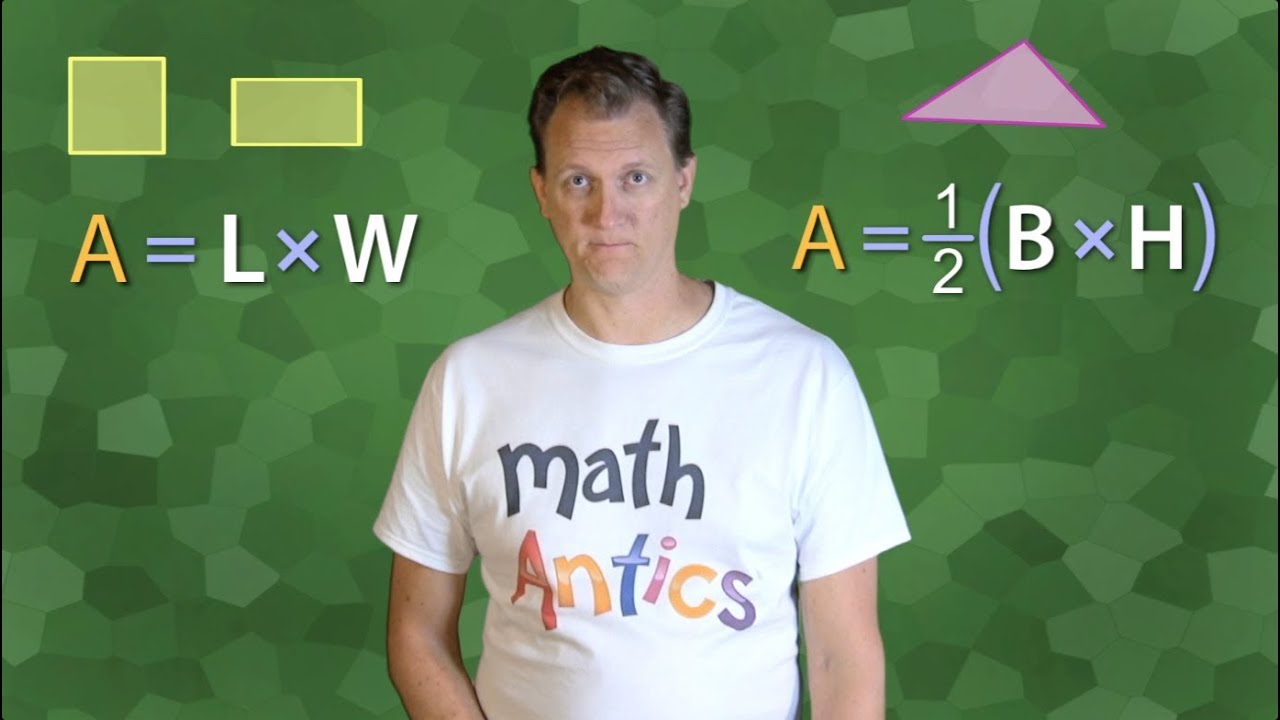
Math Antics - Area
5.0 / 5 (0 votes)
