Ecuaciones diferenciales | Introducción
Summary
TLDREste script de video ofrece una introducción al curso de ecuaciones diferenciales, explicando qué son y cómo reconocerlas. Se mencionan las variables independientes y dependientes, y se enfatiza la importancia de las derivadas en su definición. El video también contrasta ecuaciones diferenciales ordinarias y en derivadas parciales, y se menciona la necesidad de encontrar una función que satisfaga una ecuación diferencial en lugar de un valor específico. Se invita a los espectadores a ver más contenido del curso para comprender mejor cómo verificar soluciones y explorar diferentes tipos de soluciones.
Takeaways
- 😀 Un curso de ecuaciones diferenciales se presenta, enfocado en enseñar sobre este tipo de ecuaciones matemáticas.
- 🔍 La definición de una ecuación diferencial se centra en que es una ecuación que incluye derivadas de una o más funciones.
- 📚 Se menciona que las ecuaciones diferenciales son reconocidas por tener variables y derivadas dentro de la misma.
- 📝 Se da un ejemplo de cómo escribir funciones, usualmente con una letra como 'x' o 't', y cómo se representan sus derivadas.
- 👉 Se destaca que resolver una ecuación diferencial implica encontrar una función que satisfaga la ecuación, en lugar de un valor numérico como en ecuaciones algebraicas.
- 🧐 Se describe el proceso de verificar si una función es solución de una ecuación diferencial, a través de la sustitución y comparación.
- 📉 Se introduce la idea de las ecuaciones diferenciales ordinarias, las cuales involucran derivadas con respecto a una sola variable independiente.
- 📈 También se mencionan las ecuaciones diferenciales en derivadas parciales, que incluyen derivadas parciales con respecto a múltiples variables independientes.
- 📚 Se enfatiza la importancia de entender las diferencias entre ecuaciones diferenciales ordinarias y en derivadas parciales.
- 👨🏫 El guión invita a los espectadores a seguir aprendiendo sobre ecuaciones diferenciales a través de futuras lecciones y videos.
- 👋 El guión termina con un mensaje de despedida y animación a suscribirse, comentar, compartir y dar like al video.
Q & A
¿Qué es una ecuación diferencial y cómo se reconoce?
-Una ecuación diferencial es una ecuación que relaciona una función con sus derivadas. Se reconoce por tener una o más derivadas de una función dentro de la ecuación, generalmente escritas como 'f'(x)', 'f''(x)', etc., donde 'f' representa la función y 'x' es la variable independiente.
¿Cómo se diferencia una ecuación de una ecuación diferencial?
-Una ecuación diferencial siempre incluirá derivadas de una función, mientras que una ecuación en general puede no tener derivadas. Por ejemplo, 5x = 7 es una ecuación, pero no es una ecuación diferencial porque no incluye derivadas.
¿Cuál es la diferencia entre las variables independientes y las variables dependientes en una ecuación diferencial?
-Las variables independientes son las que no están definidas en términos de otras variables en la ecuación, como 'x' o 't'. Las variables dependientes, por otro lado, son funciones de las variables independientes y suelen aparecer junto con sus derivadas en la ecuación diferencial.
¿Cómo se escribe la derivada de una función en matemáticas?
-La derivada de una función se escribe como la función seguida de una coma, por ejemplo, 'f(x)' se convierte en 'f'(x)' o 'dy/dx' si 'y' es la función dependiente y 'x' es la independiente.
¿Qué es una ecuación diferencial ordinaria y cómo se identifica?
-Una ecuación diferencial ordinaria es aquella que contiene derivadas con respecto a una sola variable independiente. Se identifica porque todas las derivadas en la ecuación son de la misma variable, como 'f'(x)', 'f''(x)', etc.
¿Qué son las ecuaciones diferenciales en derivadas parciales y cómo se diferencian de las ordinarias?
-Las ecuaciones diferenciales en derivadas parciales son aquellas que contienen derivadas parciales con respecto a más de una variable independiente. Se diferencian de las ecuaciones diferenciales ordinarias porque incluyen derivadas con respecto a múltiples variables, como '∂²z/∂x∂y'.
¿Cómo se resuelve una ecuación diferencial?
-Para resolver una ecuación diferencial, se busca encontrar una función que satisfaga la ecuación. Esto implica reemplazar la función propuesta en la ecuación y verificar si las derivadas calculadas coinciden con las del lado derecho de la ecuación.
¿Cómo se verifica si una función es una solución de una ecuación diferencial?
-Para verificar si una función es una solución de una ecuación diferencial, se calcula la derivada de la función y se compara con el lado derecho de la ecuación. Si ambas partes son iguales, entonces la función es una solución.
¿Cuáles son algunos ejemplos de variables independientes comunes en ecuaciones diferenciales?
-Algunas variables independientes comunes en ecuaciones diferenciales incluyen 'x', 't', 'u', 'v', y 'y'. Estas variables generalmente representan el tiempo o una medida de longitud o distancia en diferentes contextos.
¿Por qué es importante la derivada en la resolución de ecuaciones diferenciales?
-La derivada es crucial en la resolución de ecuaciones diferenciales porque describe cómo cambia una función con respecto a su variable independiente. Conocer las derivadas es esencial para encontrar la función que satisface la ecuación diferencial dada.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Ecuaciones diferenciales simples

Ecuaciones Cuadráticas - de Segundo grado | Introducción

Solución de ecuaciones | Resolver una ecuación | Introducción

Sistemas de ecuaciones lineales 2x2 INTRODUCCIÓN

Orden de una Ecuación Diferencial
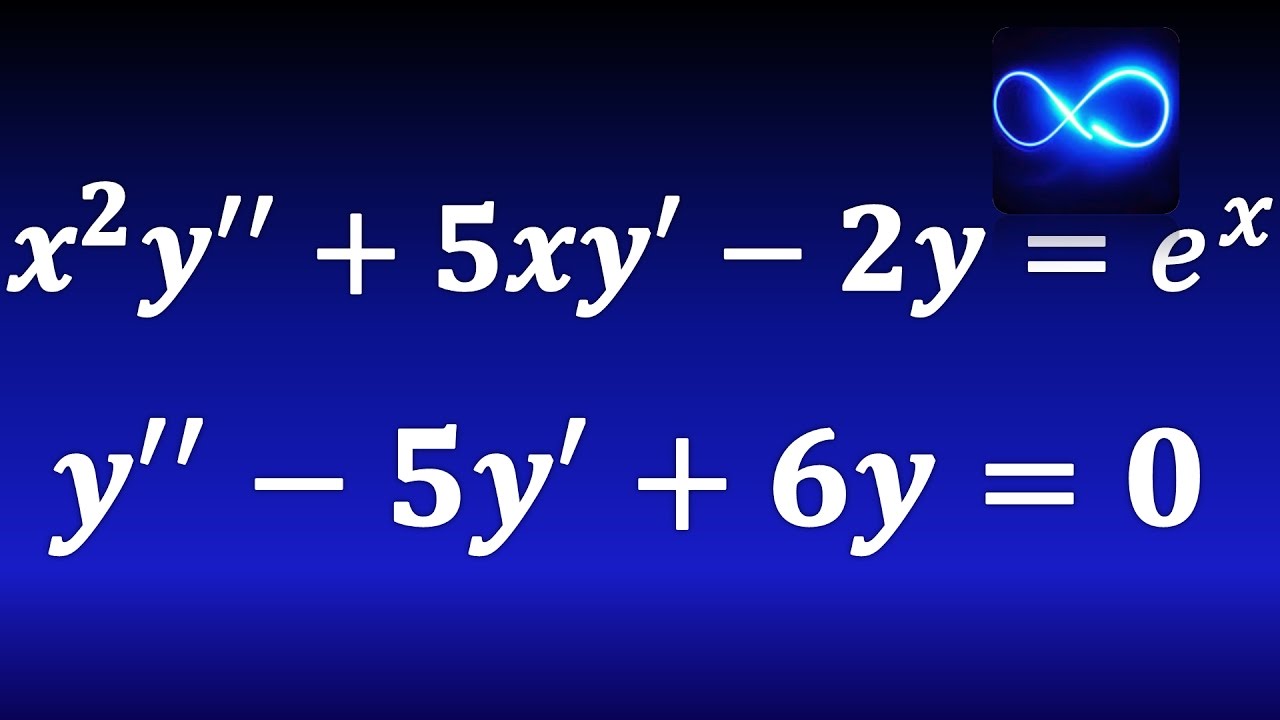
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes
5.0 / 5 (0 votes)
