Ordinary Differential Equations (ODEs) | Fundamentals of Orbital Mechanics 2
Summary
TLDRThis video dives deep into orbital mechanics, focusing on the relationship between acceleration, velocity, and position. Using Newton's second law and integration techniques, the video explains how to calculate spacecraft trajectories and solve for their orbital states. It covers both simple cases like circular orbits and complex ones like elliptical orbits. The tutorial includes a Python script for visualizing these relationships and provides insights into numerical integration methods, specifically ordinary differential equation (ODE) solvers. The video also highlights the role of the Space Engineering Podcast, offering further resources for viewers.
Takeaways
- 😀 Newton's Second Law is central to calculating spacecraft trajectories by determining accelerations caused by forces in orbital mechanics.
- 🚀 Acceleration is the first derivative of velocity and the second derivative of position with respect to time, crucial for solving orbital trajectories.
- 📚 Integration of acceleration equations allows us to calculate position and velocity over time, which are essential for modeling spacecraft motion.
- ⚙️ Ordinary differential equations (ODEs) describe the relationship between position, velocity, and acceleration in orbital mechanics, allowing for numerical solutions.
- 💻 Python is used to numerically integrate ODEs and simulate orbital motion, with libraries like numpy for calculations and matplotlib for visualization.
- 🌍 Newton's Universal Law of Gravitation is used to calculate the gravitational force between two bodies, affecting the acceleration of a spacecraft.
- 📊 Visualizing the relationship between acceleration, velocity, and position through plots helps to understand the dynamics of orbits.
- 🔄 The process of integrating acceleration to get velocity, and then integrating velocity to get position, is fundamental for describing orbital states.
- 🌒 In a circular orbit, both position and velocity magnitudes remain constant over time, indicating stable motion.
- 📡 Highly elliptical orbits, such as the Amolnea orbit, exhibit varying accelerations and velocities depending on the distance between the spacecraft and Earth.
Q & A
What is the relationship between acceleration, velocity, and position in orbital mechanics?
-In orbital mechanics, acceleration is the first derivative of velocity and the second derivative of position with respect to time. By integrating acceleration twice, we can calculate velocity and position over time, which are essential to determining the trajectory of a spacecraft.
How do Newton's laws help us calculate orbital trajectories?
-Newton's laws, particularly Newton's Second Law of Motion, allow us to calculate the acceleration of a spacecraft by relating forces to motion. These accelerations are crucial for determining how the spacecraft's position changes over time, which can be used to calculate orbital trajectories.
What is the significance of ordinary differential equations (ODEs) in orbital mechanics?
-Ordinary differential equations (ODEs) describe the relationships between acceleration, velocity, and position. These equations are essential in orbital mechanics because they allow us to model the motion of objects under the influence of gravitational forces, and solve for their positions and velocities over time.
What role does numerical integration play in orbital mechanics simulations?
-Numerical integration is used to solve ODEs in orbital mechanics, as they often cannot be solved analytically. By applying numerical methods, we can approximate the solution over discrete time steps, allowing us to simulate the trajectory of a spacecraft or any other object in orbit.
Why is the acceleration due to gravity greater when a spacecraft is closer to Earth?
-The acceleration due to gravity follows Newton's Universal Law of Gravitation, which states that the gravitational force is inversely proportional to the square of the distance between two objects. Thus, the closer a spacecraft is to Earth, the stronger the gravitational pull, resulting in greater acceleration.
How does a circular orbit differ from an elliptical orbit in terms of acceleration and velocity?
-In a circular orbit, the acceleration and velocity remain constant over time. In contrast, in an elliptical orbit, both acceleration and velocity vary as the spacecraft moves closer to and farther from the central body (e.g., Earth), with maximum acceleration and velocity occurring at periapsis (closest approach) and minimum values at apoapsis (farthest distance).
What are the common orbital elements used to describe the state of a spacecraft?
-The state of a spacecraft can be described using six orbital elements: three for position (x, y, z) and three for velocity (vx, vy, vz). Other methods, such as Keplerian or equinoctial orbital elements, can also be used to describe the state, depending on the context.
What is the importance of the gravitational parameter 'mu' in orbital mechanics?
-The gravitational parameter 'mu' represents the product of the gravitational constant and the mass of the central body (e.g., Earth). It is crucial in calculating the acceleration due to gravity and plays a key role in determining the orbital trajectories of objects within a gravitational field.
How does the concept of acceleration, velocity, and position play into Python-based orbital simulations?
-In Python-based orbital simulations, acceleration, velocity, and position are key variables that define the motion of objects. By using libraries like NumPy and Matplotlib, these variables can be calculated and plotted over time, allowing for the visualization of orbital trajectories and the analysis of the relationships between them.
What is the role of ordinary differential equation (ODE) solvers in orbital mechanics simulations?
-ODE solvers are used to numerically solve the differential equations that govern the motion of spacecraft and other objects in orbit. These solvers allow us to compute the spacecraft's position and velocity over time by integrating the equations of motion, which is essential for accurate orbital predictions.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Simple Harmonic Motion(SHM) - Graphs of Position, Velocity, and Acceleration
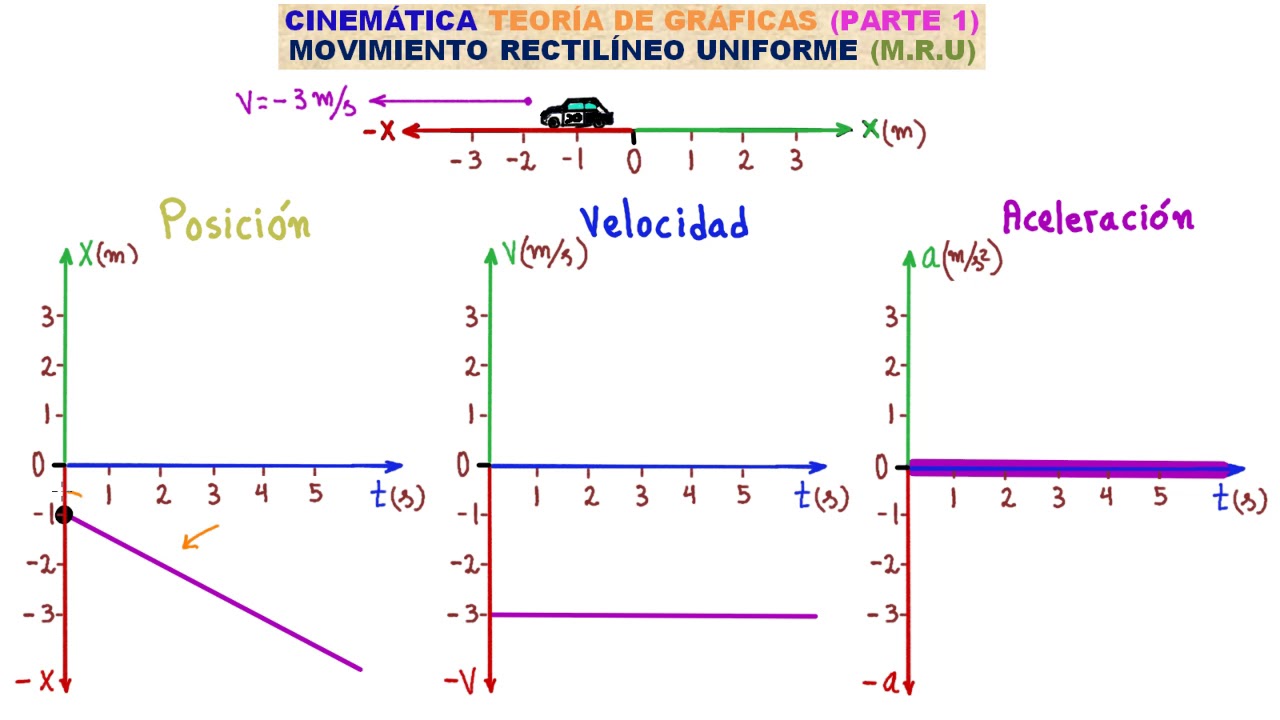
CINEMÁTICA. GRÁFICAS DEL M.R.U TEORÍA 1 [APRENDE LOS GRÁFICOS DE POSICIÓN, VELOCIDAD Y ACELERACIÓN]

Kinematic Equations in One Dimension | Physics with Professor Matt Anderson | M2-04
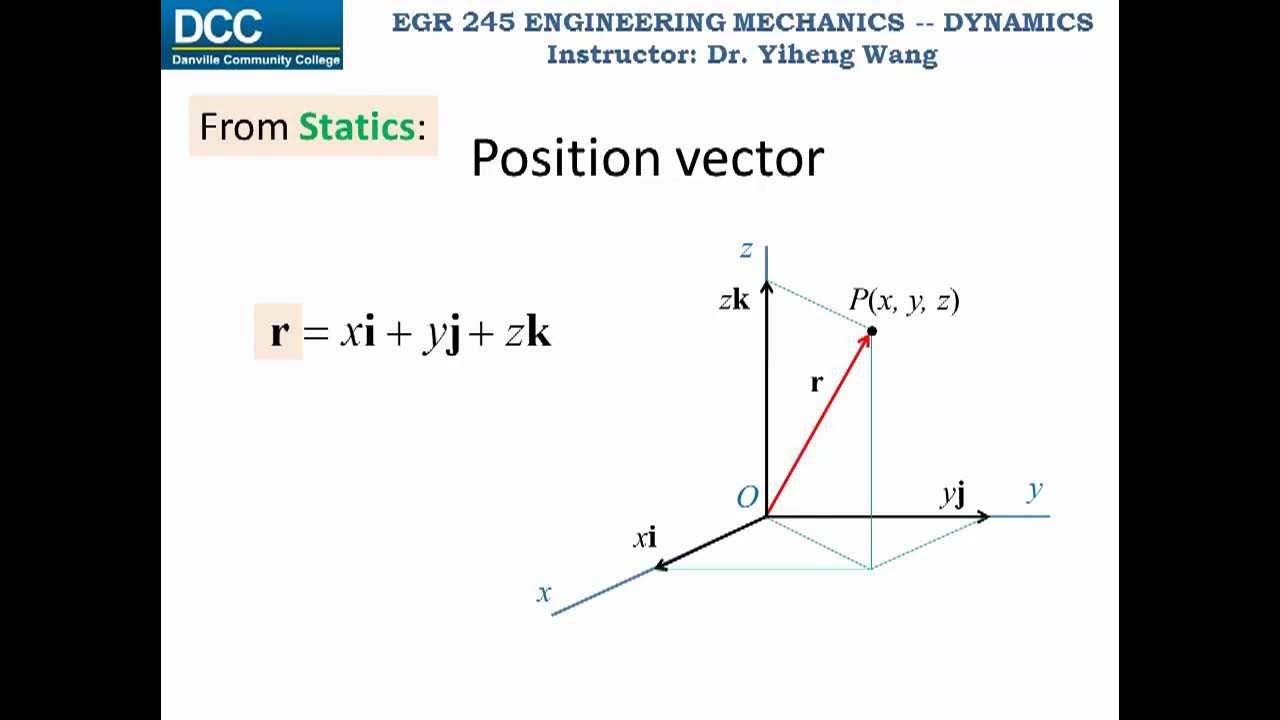
Dynamics Lecture 02: Particle kinematics, Rectilinear continuous motion part 1

Worked example: motion problems (with definite integrals) | AP Calculus AB | Khan Academy

Vektor Posisi, Kecepatan, dan Percepatan | Kinematika 2D & 3D | Part 1 | Fisika Dasar
5.0 / 5 (0 votes)
