TEORÍA DE COJUNTOS, Diferencia Simétrica

Las Pesadillas de Darío

30 Jul 202202:47

Summary

TLDREn este video, Raúl, un profesor de matemáticas, explica el concepto de diferencia simétrica entre conjuntos. A través de un ejemplo práctico con los conjuntos A y B, ilustra cómo identificar los elementos exclusivos de cada conjunto y cómo unirlos para formar la diferencia simétrica. Utilizando diagramas de Venn y mostrando paso a paso el cálculo de los elementos, Raúl hace que el tema de conjuntos sea más comprensible. Al final, se despide, mencionando que Darío no está muy interesado en este tema, sugiriendo que mejor lo repasen en otra ocasión.

Takeaways

😀 Se explica el concepto de diferencia simétrica entre dos conjuntos, que es el conjunto formado por los elementos que pertenecen a A o B, pero no a la intersección de ambos.
😀 La diferencia simétrica se representa simbólicamente como A Δ B.
😀 El conjunto A Δ B contiene los elementos de A que no están en B, y los elementos de B que no están en A.
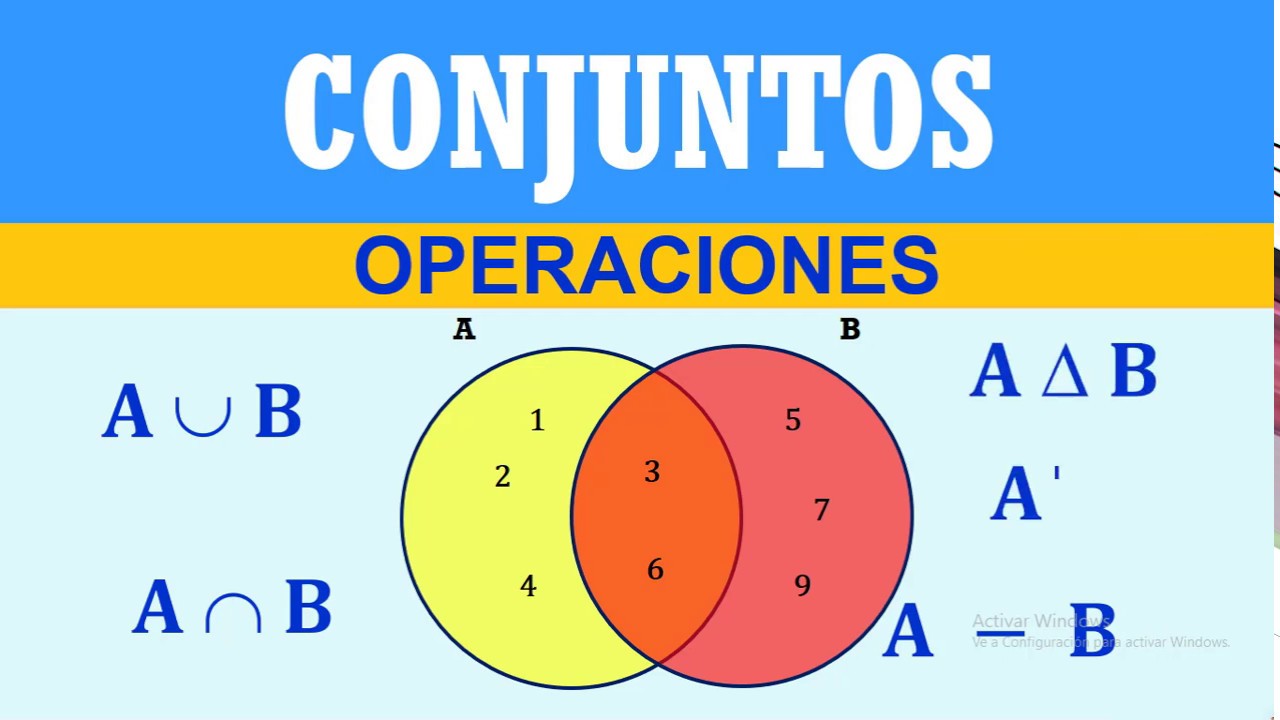
😀 Un diagrama de Venn se usa para ilustrar la diferencia simétrica entre dos conjuntos.
😀 En el ejemplo, se tienen dos conjuntos: A = {1, 2, 3, 4, 8} y B = {2, 10, 12, 7, 9}.
😀 Para encontrar la diferencia simétrica, primero se calcula A - B, que da {3, 4, 8}.
😀 Luego se calcula B - A, que da {10, 7, 9}.
😀 Finalmente, se unen A - B y B - A, lo que da el conjunto A Δ B = {3, 4, 8, 10, 7, 9}.
😀 El resultado final son los elementos que están en A o B, pero no en ambos al mismo tiempo.
😀 El profesor menciona que Darío no le gusta mucho el tema de los conjuntos, por lo que se sugiere ver el tema en otra oportunidad.

Q & A

¿Qué es la diferencia simétrica entre dos conjuntos?
-La diferencia simétrica entre dos conjuntos A y B es el conjunto formado por los elementos que pertenecen a A o a B, pero no a la intersección de A y B. Es decir, los elementos que solo pertenecen a A o solo a B, pero no a ambos.
¿Cómo se representa simbólicamente la diferencia simétrica?
-La diferencia simétrica se representa simbólicamente como A Δ B o A Δ B, lo cual significa el conjunto de los elementos que están en A o en B, pero no en su intersección.
¿Qué significa A Δ B en términos de la teoría de conjuntos?
-A Δ B es el conjunto formado por los elementos que pertenecen a A pero no a B, unidos con los elementos que pertenecen a B pero no a A.
¿Cómo se describe la diferencia simétrica en un diagrama de Venn?
-En un diagrama de Venn, la diferencia simétrica entre dos conjuntos se representa como el área rayada, que cubre las partes de A y B que no se superponen, es decir, las partes que están solo en A o solo en B.
¿Cuáles son los elementos que pertenecen a A pero no a B en el ejemplo dado?
-En el ejemplo, el conjunto A es {1, 2, 3, 4, 8} y el conjunto B es {2, 10, 12, 7, 9}. Los elementos de A que no pertenecen a B son {1, 3, 4, 8}.
¿Cuáles son los elementos que pertenecen a B pero no a A en el ejemplo dado?
-Los elementos de B que no pertenecen a A son {10, 12, 7, 9}.
¿Cómo se obtiene la diferencia simétrica entre A y B en el ejemplo?
-La diferencia simétrica se obtiene uniendo los elementos de A que no están en B ({1, 3, 4, 8}) con los elementos de B que no están en A ({10, 12, 7, 9}). El conjunto resultante es {1, 3, 4, 8, 10, 12, 7, 9}.
¿Por qué se eliminan los elementos comunes de A y B en la diferencia simétrica?
-Los elementos comunes a A y B se eliminan de la diferencia simétrica porque esta operación busca solo los elementos que están en uno de los conjuntos, pero no en ambos. Los elementos comunes no cumplen con esta condición.
¿Qué se entiende por la 'intersección' de dos conjuntos?
-La intersección de dos conjuntos A y B es el conjunto formado por los elementos que pertenecen tanto a A como a B al mismo tiempo.
¿Qué importancia tiene la diferencia simétrica en el estudio de la teoría de conjuntos?
-La diferencia simétrica es una operación importante en teoría de conjuntos porque permite identificar y trabajar con los elementos que son exclusivos de dos conjuntos, sin tener en cuenta los elementos comunes, lo cual es útil en diversas aplicaciones matemáticas y lógicas.