[SER222] M03_02 Introduction (2/2): Traversing Trees [2019; v7]
Summary
TLDREn este video, el presentador explica cómo recorrer un árbol binario utilizando tres algoritmos comunes: Preorden, Inorden y Postorden. Cada uno de estos métodos define un orden específico para visitar los nodos del árbol, siendo Preorden el que comienza por la raíz, Inorden que visita primero el subárbol izquierdo, y Postorden que visita el subárbol izquierdo y derecho antes de la raíz. A través de ejemplos prácticos y explicaciones sobre recursión, se muestra cómo aplicar estos algoritmos para explorar árboles binarios de manera eficiente, destacando su importancia en la informática.
Takeaways
- 😀 Los árboles binarios tienen una estructura jerárquica con nodos que se ramifican hacia nodos hijos, lo que difiere de estructuras lineales como las listas enlazadas.
- 😀 La traversabilidad de un árbol binario requiere algoritmos específicos para visitar todos sus nodos, ya que los árboles tienen nodos hijos izquierdo y derecho, lo que implica elecciones en el recorrido.
- 😀 Hay tres algoritmos principales para recorrer un árbol binario: preorden, inorden y postorden. Cada uno tiene un orden diferente para visitar los nodos.
- 😀 El algoritmo de recorrido en preorden visita primero la raíz, luego el subárbol izquierdo, y finalmente el subárbol derecho.
- 😀 El recorrido en inorden visita primero el subárbol izquierdo, luego la raíz, y finalmente el subárbol derecho.
- 😀 El recorrido en postorden visita primero el subárbol izquierdo, luego el subárbol derecho, y finalmente la raíz.
- 😀 En el recorrido en preorden, si se tiene un árbol con nodos A, B y C, el orden de visita sería A, B, C.
- 😀 El recorrido en inorden de un árbol con los mismos nodos (A, B y C) sería B, A, C.
- 😀 En el recorrido en postorden, el orden sería B, C, A.
- 😀 Los árboles binarios requieren el uso de funciones recursivas para recorrer cada subárbol de acuerdo con el algoritmo correspondiente, como en el caso de preorden.
- 😀 Aunque es posible hacer los recorridos de manera manual siguiendo los pasos, también se puede utilizar una aproximación visual recorriendo los nodos desde la raíz hacia abajo, tocando cada nodo según el algoritmo.
Q & A
¿Qué problema se está resolviendo en este video?
-El problema que se está resolviendo es cómo recorrer (traversar) un árbol binario y visitar todos sus nodos de manera eficiente.
¿Por qué es más complicado recorrer un árbol en comparación con una lista enlazada?
-Un árbol tiene nodos con ramas hacia la izquierda y la derecha, lo que requiere tomar decisiones sobre qué lado visitar primero. En una lista enlazada, la estructura es lineal, por lo que no hay que tomar decisiones.
¿Cuáles son los tres algoritmos principales para recorrer un árbol binario?
-Los tres algoritmos principales para recorrer un árbol binario son: Preorden, Inorden y Postorden.
¿En qué consiste el recorrido en Preorden?
-El recorrido en Preorden visita primero el nodo raíz, luego recorre el subárbol izquierdo, y finalmente el subárbol derecho.
¿Cómo se realiza un recorrido en Inorden?
-En el recorrido Inorden, se visita primero el subárbol izquierdo, luego el nodo raíz, y finalmente el subárbol derecho.
¿Qué caracteriza al recorrido en Postorden?
-En el recorrido Postorden, se visita primero el subárbol izquierdo, luego el subárbol derecho, y finalmente el nodo raíz.
¿Cuál es la diferencia principal entre los tres algoritmos de recorrido?
-La diferencia principal radica en el orden en que se visitan los nodos: Preorden visita la raíz primero, Inorden la visita en el medio, y Postorden la visita al final.
¿Cómo se utiliza la recursión en estos algoritmos?
-Cada algoritmo recursivo llama a la función para recorrer el subárbol izquierdo y derecho, repitiendo el proceso hasta que se alcanza un nodo sin hijos.
¿Qué es lo que varía al recorrer el mismo árbol con diferentes algoritmos?
-Lo que varía es el orden en que se visitan los nodos, aunque todos los algoritmos visitan todos los nodos del árbol.
¿Cuál es una forma más sencilla de visualizar un recorrido Preorden sin escribir la recursión?
-Una forma más sencilla es seguir el árbol desde la raíz y escribir los nodos a medida que se tocan en el recorrido Preorden, moviéndose en sentido antihorario.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

[SER222] M03_02 Implementation (5/10): The Min Operation

Cómo funciona: Modelo de Motor V8
34 - Árboles Binarios de Búsqueda, Creación e Inserción (EDDJava)

How Flutter renders Widgets
40 - Árboles Binarios de Búsqueda, Eliminar un Nodo, Implementación (EDDJava)
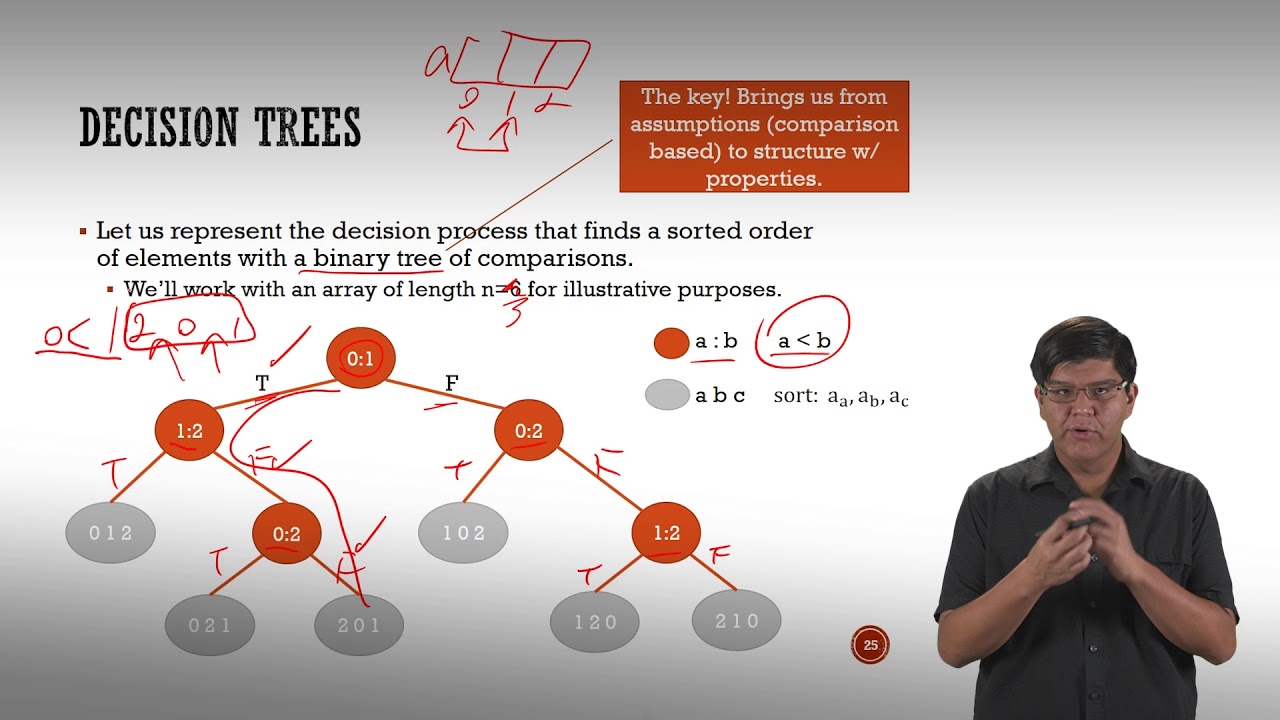
[SER222] M02_02 The Sorting Lower Bound (2/4): Decision Trees
5.0 / 5 (0 votes)
