Limite de una Función con Valor Absoluto en el Denominador Límites Algebraicos Límite en un Punto
Summary
TLDR本视频讲解了如何计算函数在特定点的极限,重点是对函数 f(x) = 5x / |x + 4| 在 x = -4 处的极限进行分析。通过计算左右极限,我们发现无论从右边还是左边逼近,极限都趋向于负无穷。因此,该点的极限不存在。视频通过详细的步骤和图示,帮助理解极限的计算过程,特别是如何处理绝对值函数的分母为零的情况。
Takeaways
- 😀 计算极限时,要检查左右极限是否相等,并且它们的值应该是有限的,而不是无限大的。
- 😀 本题中,我们计算的是当 x 趋近于 -4 时,函数 5x / |x + 4| 的极限。
- 😀 函数 f(x) = 5x / |x + 4| 在 x = -4 时不定义,因为在该点分母为零。
- 😀 为了验证极限是否存在,必须计算右侧和左侧的极限,并确保它们相等且是有限的。
- 😀 右侧极限(x > -4)时,|x + 4| 等于 x + 4,因此极限为 -∞。
- 😀 左侧极限(x < -4)时,|x + 4| 等于 -(x + 4),计算结果也是 -∞。
- 😀 因为右侧和左侧的极限都趋向于 -∞,所以函数在 x = -4 处的极限是 -∞。
- 😀 由于左右极限都趋向于 -∞,而不是一个有限值,函数在 x = -4 处的极限不存在。
- 😀 图形上,函数在 x = -4 附近会趋向于 -∞,不论是从右侧还是左侧。
- 😀 总结:如果左右极限相等且为有限值,函数在该点的极限才存在;否则,极限不存在。
Q & A
什么是绝对值函数?
-绝对值函数是指将一个数的负值转换为正值,例如,|x + 4| 会根据 x + 4 的符号而表现不同:当 x + 4 ≥ 0 时,|x + 4| = x + 4;当 x + 4 < 0 时,|x + 4| = -x - 4。
在本例中,为什么函数在 x = -4 处没有定义?
-函数 f(x) = 5x / |x + 4| 在 x = -4 处没有定义,因为当 x = -4 时,|x + 4| = 0,导致分母为 0,除以零是没有定义的。
什么是侧限的概念?
-侧限是指当 x 接近某个特定值时,函数从左侧(x 值比该点小)或右侧(x 值比该点大)趋近的极限值。侧限要求左侧极限和右侧极限相等且有限,才能得出该点的极限值。
如何计算右侧极限?
-右侧极限是指当 x 从比 -4 大的值趋近 -4 时的极限。在本例中,x > -4 时,|x + 4| = x + 4,因此函数成为 5x / (x + 4),计算得右侧极限是负无穷。
如何计算左侧极限?
-左侧极限是指当 x 从比 -4 小的值趋近 -4 时的极限。在本例中,x < -4 时,|x + 4| = -x - 4,因此函数成为 5x / (-x + 4),计算得左侧极限也是负无穷。
为何右侧和左侧的极限都为负无穷?
-当 x 接近 -4 时,分母趋近于零,而分子恒为负数。无论是从右侧接近还是左侧接近,结果都是负无穷。这是因为分子和分母的符号始终使得最终结果为负无穷。
什么情况下函数的极限不存在?
-当函数的左右极限不相等,或者其中一个极限是无限大的情况下,函数在该点的极限就不存在。在本例中,左右极限都为负无穷,因此极限不存在。
为什么说这个极限是无穷大的?
-这个极限是无穷大的,因为当 x 接近 -4 时,分母的绝对值接近零,而分子始终是负数,因此值会趋近于负无穷。这表明极限不存在且趋向无穷。
如何通过图形理解这个极限?
-通过图形可以看到,当 x 接近 -4 时,函数的值会快速下降到负无穷。在 -4 处,函数没有定义,因此图形在这个点有一个断点,且从左侧和右侧都趋向负无穷。
如果极限存在,会有什么样的结果?
-如果极限存在,左右极限必须相等,并且应该是一个有限的数值。如果存在且是有限的,那么可以给出一个具体的极限值。如果是无穷大或无穷小,则说明极限不存在。
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Funciones pares e impares explicación gráfica

03. Derivative using definition as limit

Límites cuando x tiende al infinito | Profe Andalón

Cálculo Integral 02:Sumas infinitas. Infinite sums.
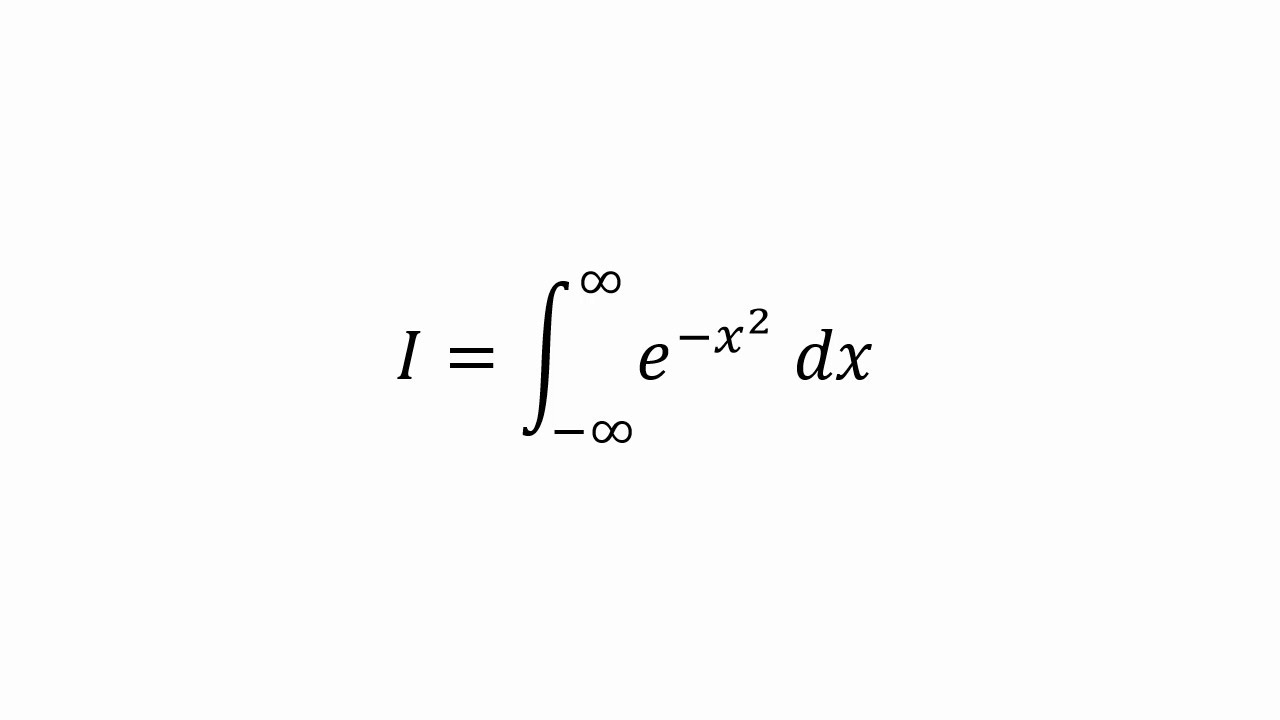
The Gaussian Integral

Teorema fundamental del cálculo: definición y ejemplos

Varberg《Calculus》微积分 Chapter 1 Limits #3 |无穷小
5.0 / 5 (0 votes)
