Konsep Metode Newton

Summary

This video explains Newton's method, a numerical technique used to find the roots of a function. Unlike the bisection method, which divides intervals, Newton's method begins with an initial guess and uses tangents to iteratively approximate the root. The video demonstrates the process with a step-by-step example, showing how the method converges to the correct solution, achieving high accuracy. It also includes a practical implementation of the method, emphasizing the use of derivatives and iterating until the error is within the desired tolerance.

Takeaways

• 😀 The Newton's method is used for finding the root of a function, just like the bisection method, but with a simpler process.
• 😀 Unlike the bisection method, Newton's method requires an initial guess or starting point for the root (X1).
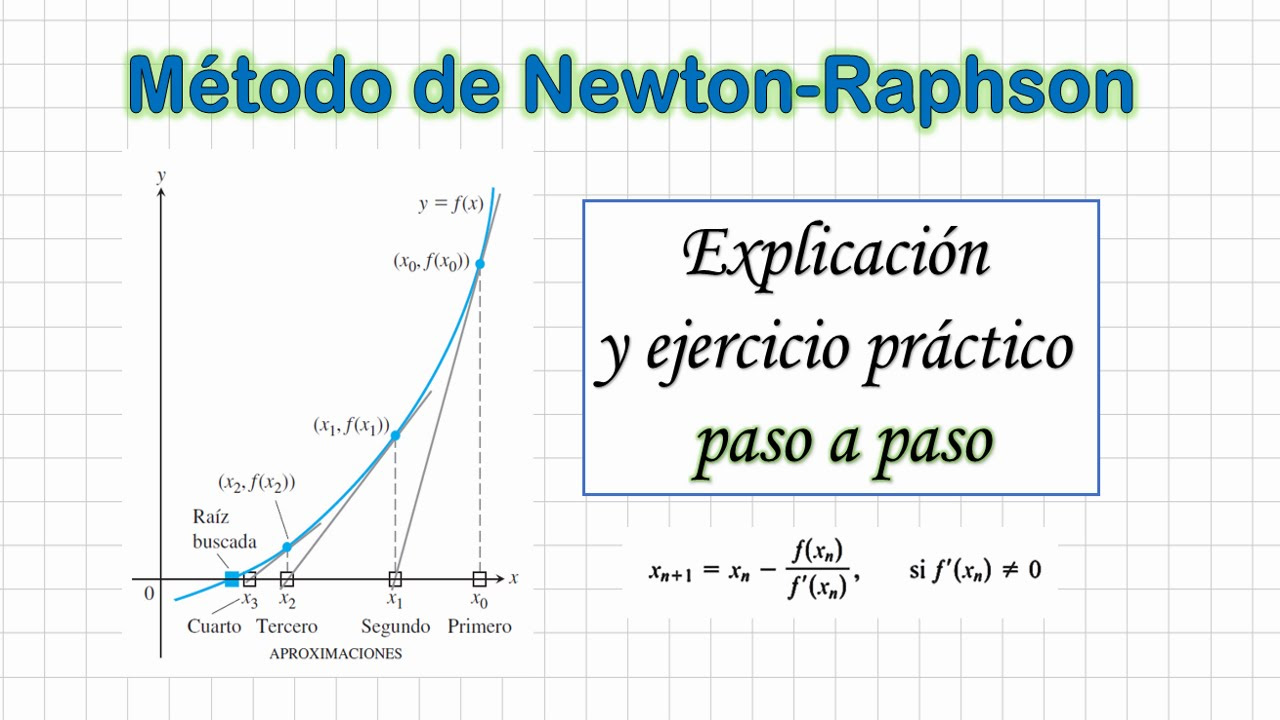
• 😀 The method uses tangent lines to estimate the root by iterating the process and improving the approximation with each step.
• 😀 Newton's method involves drawing tangent lines at successive points on the curve of the function, helping to zero in on the root.
• 😀 The method requires both the function and its derivative (first derivative) to calculate the next approximation.
• 😀 Each iteration of Newton's method provides a better estimate of the root, with the error decreasing progressively.
• 😀 A crucial element of the method is ensuring that the error between successive estimates is smaller than a predefined tolerance (e.g., 10^-4).
• 😀 The formula for each iteration in Newton’s method is: Xn+1 = Xn - f(Xn) / f'(Xn).
• 😀 An example of Newton's method is solving the equation x^3 - 2x^2 - 5 = 0, with an initial guess of X1 = 2.
• 😀 The process of using Newton’s method continues until the error becomes sufficiently small (less than the tolerance), indicating convergence to the root.

Q & A

What is the main purpose of Newton's Method?

Newton's Method is used to find the roots of a real-valued function by approximating the solutions through iterative steps. It aims to refine an initial guess and converge to the actual root of the function.

How does Newton's Method differ from the Bisection Method?

Unlike the Bisection Method, which divides an interval and narrows down the range in which the root lies, Newton's Method starts with an initial guess and iteratively improves the estimate using tangents to the function. Newton's Method can converge more quickly if the initial guess is close to the root.

What is the key concept behind Newton's Method?

The key concept behind Newton's Method is using the tangent line at the current approximation of the root to estimate the next approximation. This process repeats until the estimates converge to the root of the function.

What formula is used in Newton's Method?

The formula used in Newton's Method is: x_{n+1} = x_n - rac{f(x_n)}{f'(x_n)} where f(x_n) is the value of the function at x_n, and f'(x_n) is the derivative of the function at x_n.

Why is choosing a good initial guess important in Newton's Method?

A good initial guess is crucial in Newton's Method because the method relies on the tangent line of the function at that guess to iteratively refine the solution. If the initial guess is too far from the actual root, the method may diverge or converge to a different root.

What does the error term represent in Newton's Method?

The error term represents the difference between successive approximations of the root. As the iterations proceed, the error decreases, and the approximations become more accurate until they fall below a predetermined tolerance.

What does it mean for Newton's Method to 'converge'?

For Newton's Method to converge, the sequence of approximations (x_n) must approach the actual root of the function as the number of iterations increases. The process stops when the error between successive approximations becomes smaller than the chosen tolerance.

Can Newton's Method always be used to find the root of a function?

No, Newton's Method does not always converge. If the initial guess is too far from the root, or if the function has certain types of behavior (such as a flat slope or singularities), the method may not converge, or it might converge to the wrong root.

In the provided example, what function was solved using Newton's Method?

In the provided example, the function solved using Newton's Method was: f(x) = x^3 - 2x^2 - 5

What is the significance of the derivative in Newton's Method?

The derivative of the function is used in Newton's Method to calculate the slope of the tangent line at each approximation. This slope helps determine the next approximation by indicating the direction in which the root lies.