SOLVING PROBLEMS USING VENN DIAGRAM || GRADE 7 MATHEMATICS Q1

Summary

In this video, the concepts of set notation and Venn diagrams are explored through real-life examples and problem-solving techniques. Key operations such as union, intersection, complement, and difference are explained using social media accounts and student test results. The video demonstrates how to translate everyday scenarios into set notation, calculate cardinality, and solve problems by analyzing overlapping sets. By understanding these fundamental set operations, viewers will be able to approach and solve a wide range of set-related problems effectively.

Takeaways

• 😀 Venn diagrams are used to visualize relationships between different sets, showing how they intersect, unite, and differ.
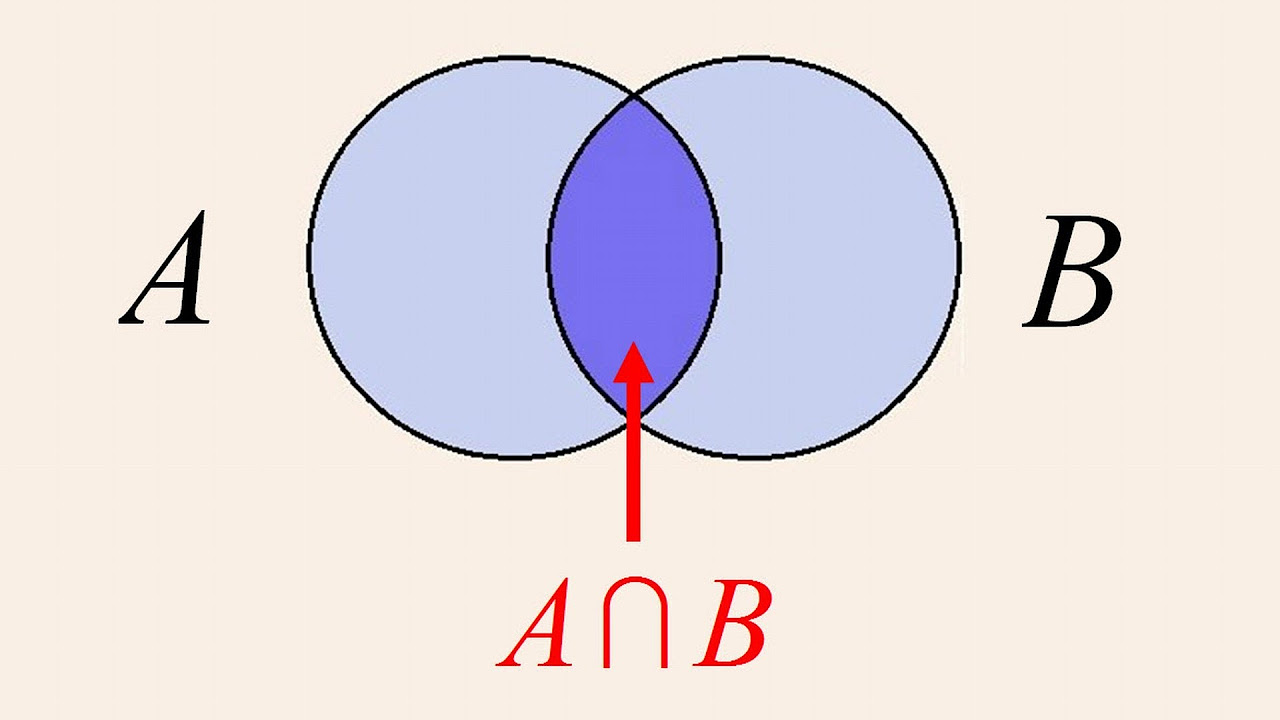
• 😀 Set notation is key to expressing set operations like union (A ∪ B), intersection (A ∩ B), and difference (A - B).
• 😀 The union of two sets includes all the elements from both sets, while the intersection only includes common elements.
• 😀 The difference of two sets (A - B) includes elements from A that are not in B.
• 😀 The complement of a set represents all elements not included in the set.
• 😀 Words like 'and' or 'all three' indicate intersection in set notation.
• 😀 'Or' refers to the union of sets, and 'but not' signifies the complement or difference.
• 😀 Cardinality refers to the number of elements in a set, and is often represented by the symbol |A|.
• 😀 Real-world problems can be solved using Venn diagrams, such as finding the number of people with certain social media accounts.
• 😀 For example, in a social media survey, we can calculate how many people have Facebook, Twitter, Instagram, or combinations of these accounts.
• 😀 Venn diagrams can also be used to solve problems involving students passing tests, like math and science, by visualizing the overlaps and differences.

Q & A

What does the intersection of two sets represent in a Venn diagram?

The intersection of two sets, denoted as A ∩ B, represents the elements that are common to both sets. In a Venn diagram, this is shown by the area where the two sets overlap.

How do you express the union of two sets using set notation?

The union of two sets, denoted as A ∪ B, includes all elements that are in either set A, set B, or both. In a Venn diagram, this is represented by the entire area covered by both sets.

What is the difference between a set and its complement in a Venn diagram?

The complement of a set A, denoted as A', consists of all elements not in set A. In a Venn diagram, this is represented by the area outside of set A.

How is the difference between two sets expressed in set notation?

The difference between two sets, denoted as A - B, includes all elements that are in set A but not in set B. In a Venn diagram, this is represented by the part of A that does not overlap with B.

How do you calculate the number of people who have Facebook or Instagram accounts in the provided example?

To calculate the number of people who have either Facebook or Instagram accounts, we use the union of the two sets: F ∪ I. This involves adding all the elements in both sets, including those that belong to both Facebook and Instagram.

What does the term 'only' mean when applied to sets in Venn diagrams?

'Only' refers to the elements that belong to a specific set but not to any other set. For example, 'Facebook only' means the people who have a Facebook account but do not have Twitter or Instagram accounts.

In the example with 40 people surveyed about social media accounts, how would you represent 'Facebook and Twitter accounts' in set notation?

The phrase 'Facebook and Twitter accounts' refers to the intersection of the two sets, represented as F ∩ T in set notation. This includes the people who have both Facebook and Twitter accounts.

How do you calculate the cardinality of a set in a Venn diagram?

The cardinality of a set refers to the number of elements in the set. In a Venn diagram, you calculate the cardinality by counting the total number of elements in each region of the diagram that corresponds to the set or operation being described.

In the math and science exam problem, how do you represent the number of students who passed only the Science test?

To represent the number of students who passed only the Science test, you subtract the number of students who passed both Math and Science from the total number of students who passed Science. In set notation, this is S - M.

What does the term 'neither' refer to in the context of Venn diagrams, and how is it calculated?

The term 'neither' refers to the elements that do not belong to any of the sets involved. In a Venn diagram, it represents the area outside all sets. To calculate it, you subtract the union of all sets from the universal set, i.e., the complement of (A ∪ B ∪ C).