Cara Cepat dan Mudah Hitung Pengurangan Bilangan Biner
Summary
TLDRThis video explains binary subtraction, covering three key conditions: subtraction without borrowing, subtraction with borrowing from the left, and subtraction where borrowing isn’t possible due to encountering a '0'. The script uses examples to illustrate these scenarios, showing how borrowing and transferring bits work in binary arithmetic. The video also contrasts manual binary subtraction with computer methods, where two's complement and one's complement are typically used for efficiency. The tutorial concludes by highlighting how these binary subtraction concepts are vital for both human calculations and computer operations.
Takeaways
- 😀 Binary subtraction involves three key conditions: without borrowing, with borrowing, and impossible borrowing.
- 😀 Condition 1: Subtraction without borrowing occurs when corresponding bits are subtracted without needing to borrow from higher bits.
- 😀 Condition 2: Subtraction with borrowing happens when a '0' bit is encountered, and borrowing is required from a higher bit.
- 😀 Condition 3: Impossible borrowing occurs when no '1' exists to borrow from, so borrowing continues to higher bits.
- 😀 Binary subtraction follows the same principles as decimal subtraction but in binary form.
- 😀 In the second condition, borrowing works by converting a '0' into '10' (binary) when needed to subtract.
- 😀 The process involves moving from right to left through the binary numbers, ensuring each subtraction is accurate.
- 😀 When borrowing is required, it changes the bit value temporarily to allow the subtraction to proceed.
- 😀 In some cases, multiple bits need to be borrowed from higher positions to complete the subtraction.
- 😀 Computers often use complement arithmetic (one's and two's complement) to handle binary subtraction, which differs from manual methods.
- 😀 This video aims to explain binary subtraction for humans, with a focus on the three conditions, before moving on to complementary methods used by computers.
Q & A
What is binary subtraction?
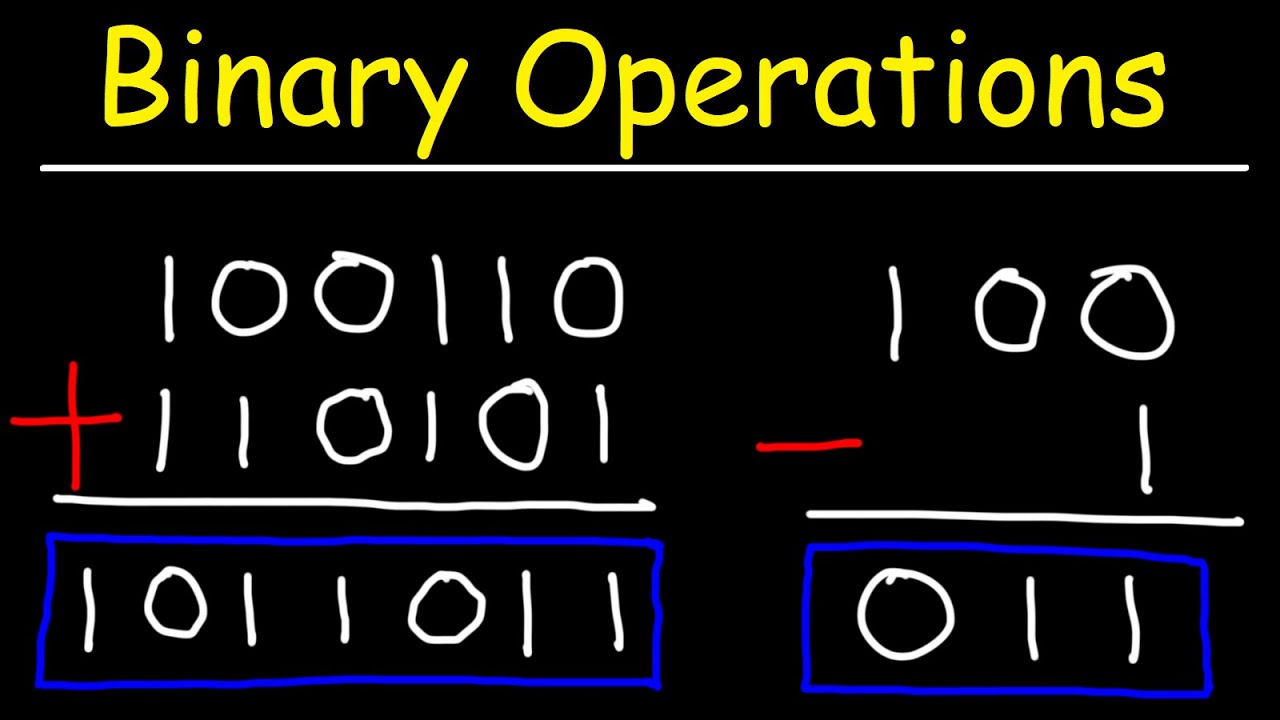
-Binary subtraction is the process of subtracting one binary number from another. It operates with only two digits, 0 and 1, and follows rules similar to decimal subtraction, with specific cases for borrowing when necessary.
What happens when you subtract 0 from 0 in binary?
-When you subtract 0 from 0 in binary, the result is 0.
What is the result of subtracting 1 from 0 in binary?
-When you subtract 1 from 0 in binary, borrowing occurs from the left bit. The result is 1 (from the borrowed bit) and 0 after borrowing.
Can you explain the first condition of binary subtraction?
-The first condition is binary subtraction without borrowing. This occurs when each corresponding bit in the two binary numbers can be directly subtracted without needing to borrow from any higher bits.
Give an example of binary subtraction without borrowing.
-An example of binary subtraction without borrowing is 11011 - 1001, which results in 100100.
What happens during binary subtraction when borrowing is needed?
-When borrowing is needed in binary subtraction, a 1 is borrowed from the next higher bit, which allows the subtraction to proceed with the borrowed bit contributing to the result.
Provide an example where binary subtraction involves borrowing.
-An example of binary subtraction with borrowing is 11101 - 1011. After borrowing from the higher bits, the result is 100100.
What is the third condition in binary subtraction?
-The third condition occurs when borrowing is not possible because the bit on the left is 0. In this case, borrowing cascades to higher bits until a 1 is found.
How does the borrowing process work when you cannot borrow from the left bit?
-When borrowing is not possible from the left bit (because it is 0), the borrow must cascade to the next higher bit that contains a 1. This borrowing process continues until the subtraction can proceed.
Why do computers use complement notation for binary subtraction instead of the direct method?
-Computers use complement notation (specifically one’s complement and two’s complement) for binary subtraction because it simplifies the subtraction process and avoids handling multiple cases of borrowing directly. This method ensures more efficient processing in digital systems.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
How To Add and Subtract Binary Numbers | Computer Science

🔴 HABILIDADE 1. SOMA e SUBTRAÇÃO entre inteiros

Subtracting Decimals Explained: A Step-By-Step Review | Understanding Decimal Subtraction

82. OCR A Level (H446) SLR13 - 1.4 Floating point arithmetic

ATURAN DASAR OPERASI MATEMATIKA

How To Convert Decimal to Binary
5.0 / 5 (0 votes)
