Persamaan Regresi Linear - Matematika Wajib SMA Kelas XI Kurikulum Merdeka
Summary
TLDRThis video continues the discussion on linear regression, focusing on how to determine the base speed line using regression equations. The presenter explains the difference between the least squares method and regression analysis, emphasizing the significance of the regression line passing through the average coordinates of the independent and dependent variables. The video outlines the formulas for calculating the coefficients 'a' and 'b' in the regression equation, illustrating the process with a practical example involving weight loss through cycling. Viewers are encouraged to practice similar problems for better understanding.
Takeaways
- 📊 The linear regression model can be determined using two methods: the least squares method and the regression equation.
- ✏️ The general form of a linear regression equation is expressed as ŷ = a + bX, where ŷ is the predicted value, X is the independent variable, a is the y-intercept, and b is the slope.
- 🔍 The regression line always passes through the average coordinates of the independent (X̄) and dependent variables (Ȳ).
- 📈 The slope (b) indicates the relationship between the variables: a positive value indicates a positive correlation, while a negative value indicates a negative correlation.
- 🧮 To find the y-intercept (a), use the formula a = Ȳ - bX̄, ensuring to calculate the means of the variables first.
- 🔢 The calculations for slope (b) involve using the formula b = (nΣXY - ΣXΣY) / (nΣX² - (ΣX)²), requiring summation of products and squares of the variables.
- 🔗 In practice, determining the regression equation simplifies data analysis by directly providing a model without requiring graphical representation.
- 🔎 Understanding which variable is independent and which is dependent is crucial to avoid errors in the regression analysis.
- 📚 The video emphasizes practicing similar problems to reinforce understanding of regression concepts.
- 🎓 The overall objective is to provide a clear and systematic method for determining the linear relationship between variables, enhancing data interpretation skills.
Q & A
What is the main topic of the video?
-The video discusses how to determine the base speed line using linear regression.
What is the formula for the linear regression equation presented in the video?
-The linear regression equation is represented as \( \hat{y} = a + bX \), where \( \hat{y} \) is the predicted dependent variable, \( a \) is the y-intercept, and \( b \) is the slope.
How does the linear regression line relate to average coordinates?
-The regression line always passes through the average coordinates of the independent and dependent variables, denoted as \( \bar{X} \) and \( \bar{Y} \).
What is the formula to calculate the y-intercept \( a \)?
-The formula to calculate \( a \) is \( a = \bar{Y} - b \cdot \bar{X} \).
How is the slope \( b \) calculated?
-The slope \( b \) is calculated using the formula: \( b = \frac{n(\Sigma XY) - (\Sigma X)(\Sigma Y)}{n(\Sigma X^2) - (\Sigma X)^2} \).
What kind of example is used to illustrate the calculation in the video?
-An example involving weight loss from cycling is used, where data is provided on the duration of cycling and the corresponding weight loss.
What are the steps to find the regression line as mentioned in the video?
-The steps include calculating necessary sums (such as \( \Sigma X \), \( \Sigma Y \), \( \Sigma XY \), and \( \Sigma X^2 \)), determining the slope \( b \), finding the intercept \( a \), and then deriving the regression equation.
What distinguishes linear regression from the least squares method according to the video?
-Linear regression allows for a direct calculation of the regression equation without the need to analyze the distribution of data points, unlike the least squares method which involves finding the best-fitting line through trial and error.
Why is it important to identify the independent and dependent variables?
-Identifying the independent (input) and dependent (output) variables is crucial to ensure correct analysis and interpretation of the data.
What final advice does the presenter give regarding practicing these calculations?
-The presenter encourages viewers to practice similar problems and use tools like calculators to facilitate the calculations involved.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

PENGERTIAN REGRESI LINEAR
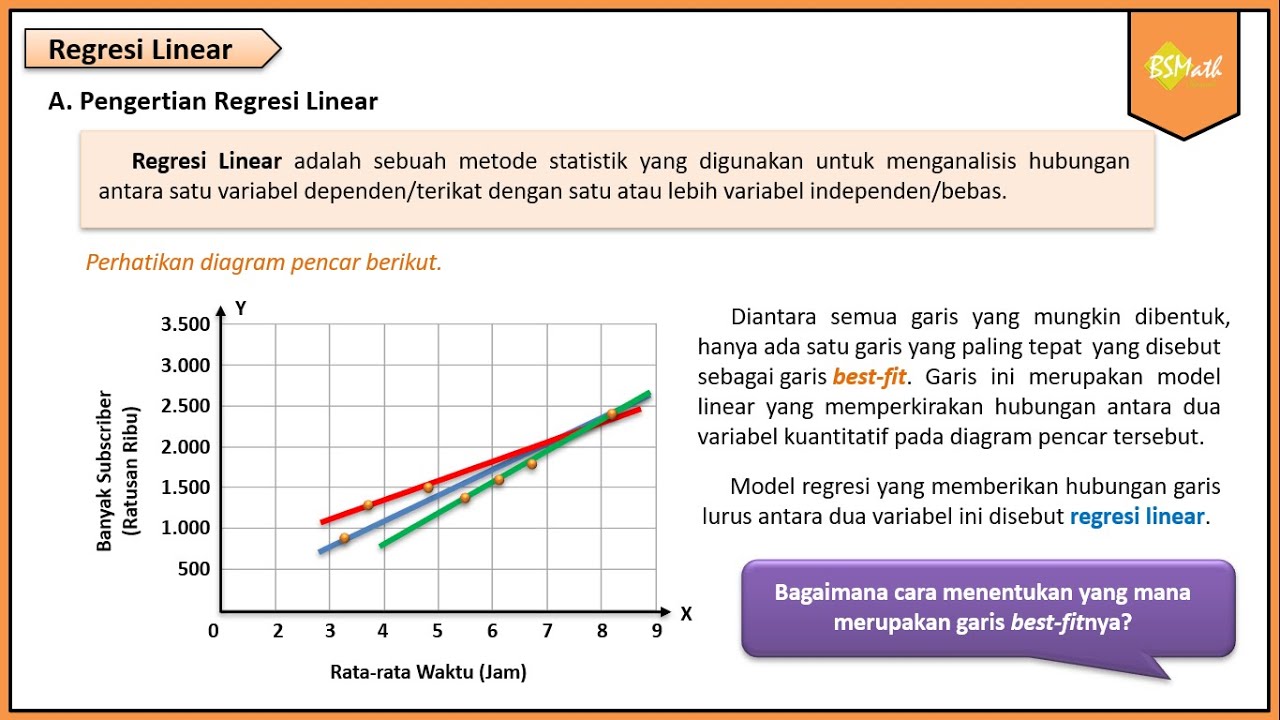
Pengertian Regresi Linear - Matematika Wajib Kelas XI Kurikulum Merdeka

Introduction to Machine Learning, Lecture-7 ( 2022 version) ( Linear Regression, Normal Equations)
Regresion Lineal

STATISTICA parte 2.3 : correlazione e regressione
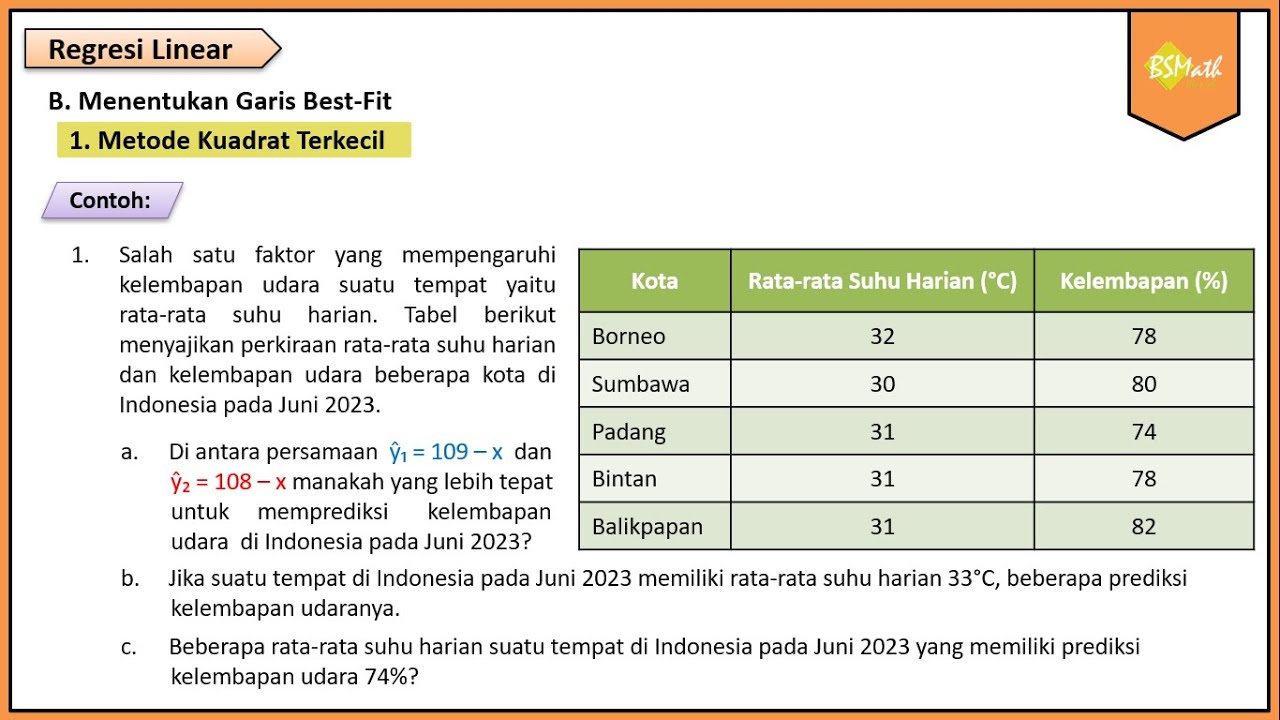
Contoh Soal dan Pembahasan Metode Kuadrat Terkecil - Matematika Wajib Kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)
