17 Momento de un Par
Summary
TLDREn este video se explora el concepto de momento de par, explicando cómo dos fuerzas de igual magnitud y dirección opuesta generan un momento alrededor de un punto. Se detallan las fórmulas para calcular el momento resultante y se demuestra que este efecto es independiente del punto de referencia. También se analizan pares equivalentes y cómo se pueden aplicar a situaciones prácticas, como en el caso de una rueda. Además, se introduce la idea de que los momentos pueden representarse como vectores libres, facilitando su manipulación y suma en diferentes contextos.
Takeaways
- 😀 El momento de par se genera por la acción de dos fuerzas de igual magnitud, dirección y sentido opuesto.
- 🤔 Para calcular el momento con respecto a un punto, se utiliza la fórmula: R1 × F1 + R2 × F2.
- 📏 La distancia (R) es crucial para determinar el momento, ya que es la distancia entre las líneas de acción de las fuerzas.
- 🔄 El momento producido por dos fuerzas paralelas de sentido contrario es el mismo, independientemente del punto donde se calcule.
- 🧮 La magnitud del momento se puede expresar como la fuerza multiplicada por la distancia perpendicular entre las líneas de acción de las fuerzas.
- ⚖️ Dos pares de fuerzas que producen el mismo momento se consideran pares equivalentes.
- 🚗 Un ejemplo práctico es aplicar un par de fuerzas a una rueda para calcular el momento producido.
- 📐 La representación vectorial de pares de fuerzas permite sumar momentos en diferentes puntos y obtener un momento resultante.
- ✏️ La dirección del momento se determina usando la regla de la mano derecha: se cruza la distancia (R) con la fuerza (F).
- 🔄 Los momentos son vectores libres, lo que significa que pueden trasladarse a diferentes posiciones sin cambiar su efecto.
Q & A
¿Qué es un momento de par en el contexto de la física?
-Un momento de par se refiere a dos fuerzas de igual magnitud y dirección, pero de sentido opuesto, que producen un efecto rotacional en un objeto.
¿Cómo se calcula el momento producido por dos fuerzas?
-El momento se calcula como la suma de los productos cruz de las distancias y las fuerzas, es decir, R1 × F1 + R2 × F2.
¿Qué significa que un momento es un 'vector libre'?
-Significa que el momento puede ser representado en cualquier punto sin cambiar su efecto, es decir, su magnitud y dirección permanecen constantes.
¿Cuál es la relación entre el ángulo y la magnitud del momento?
-La magnitud del momento es igual a la fuerza multiplicada por la distancia perpendicular entre las líneas de acción de las fuerzas y se ve afectada por el seno del ángulo entre ellas.
¿Qué condiciones deben cumplirse para que dos pares de fuerzas sean equivalentes?
-Los pares son equivalentes si la magnitud del momento producido por las fuerzas es la misma, es decir, F1 × D1 = F2 × D2.
¿Cómo afecta la distancia entre dos fuerzas al momento que producen?
-A mayor distancia entre las fuerzas, mayor será el momento producido, dado que se multiplica por la magnitud de la fuerza.
¿Qué representa el producto cruz entre R y F?
-El producto cruz R × F representa el momento en relación a un punto específico, donde R es la distancia desde ese punto a la línea de acción de la fuerza F.
¿Por qué es importante el concepto de momento en aplicaciones prácticas?
-El concepto de momento es crucial en el diseño y análisis de estructuras y mecanismos, ya que determina cómo las fuerzas afectan el movimiento y la estabilidad.
¿Cómo se relaciona el momento con el movimiento de una rueda?
-Al aplicar un par de fuerzas en una rueda, se genera un momento que provoca la rotación de la rueda, permitiendo que se mueva y realice trabajo.
¿Qué sucede si se cambia la dirección de una de las fuerzas en un par?
-Si se cambia la dirección de una de las fuerzas en un par, el momento resultante también cambiará, ya que la magnitud y la dirección del momento dependen de la configuración de las fuerzas.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Momento de un par. Fuerza y un par. Profesor Yee

Momento de fuerzas No paralelas_Teoría y Práctica_Parte 2.

Física | Momento de torsión

TEOREMA DE VARIGNON. PRINCIPIO DE MOMENTOS. TEORÍA Y CONCEPTOS DE ESTÁTICA 👨🏫

Momento de Fuerza o Torque - Ejercicios Resueltos - Intro y Explicación
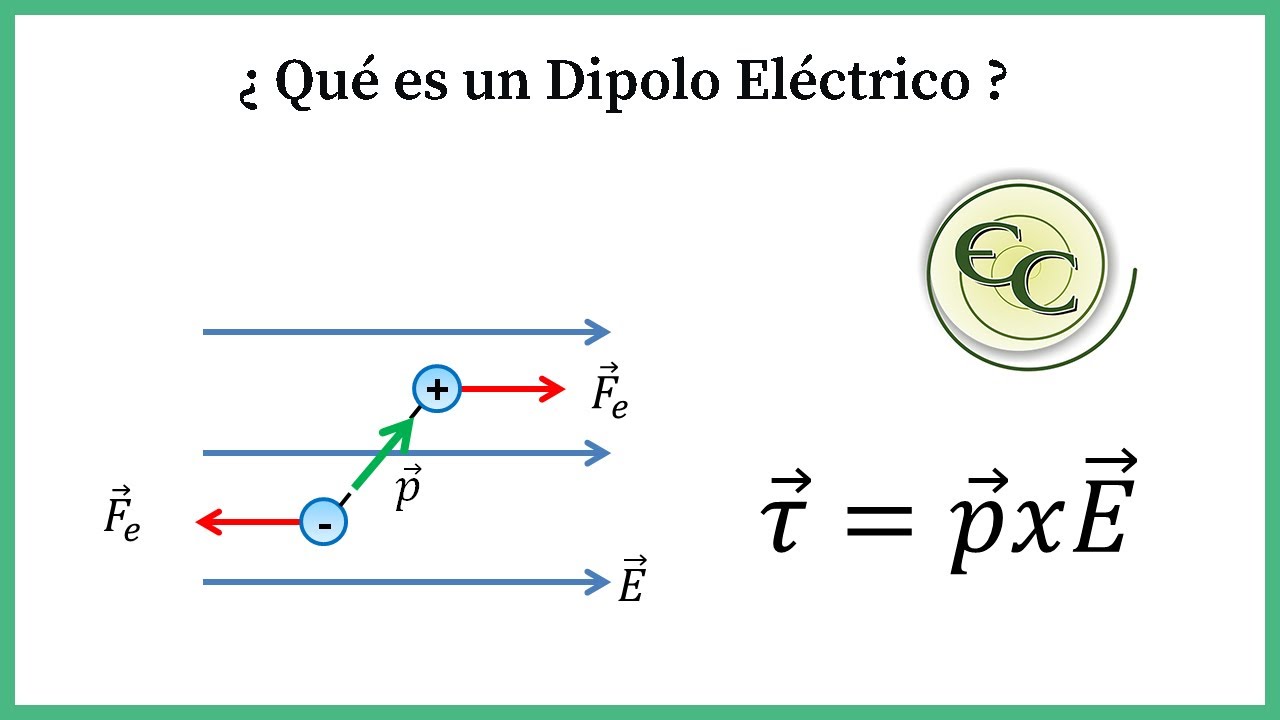
24. Dipolo electrico-Explicacion
5.0 / 5 (0 votes)
