#kongruen Kongruensi (2) - Syarat dua segitiga kongruen - Matematika SMP kelas 9
Summary
TLDRThis educational video explores the concept of triangle congruence, explaining key criteria such as SSS, SAS, ASA, AAS, and HL. Through engaging examples and practical measurements, the instructor illustrates how to determine if two triangles are congruent based on their sides and angles. Viewers learn the importance of understanding these properties for solving geometric problems, with an emphasis on practical applications and problem-solving techniques. The lesson concludes with encouragement for students to practice and deepen their comprehension of triangle congruence.
Takeaways
- 😀 Understanding triangle congruence is crucial in geometry as it helps establish relationships between triangles.
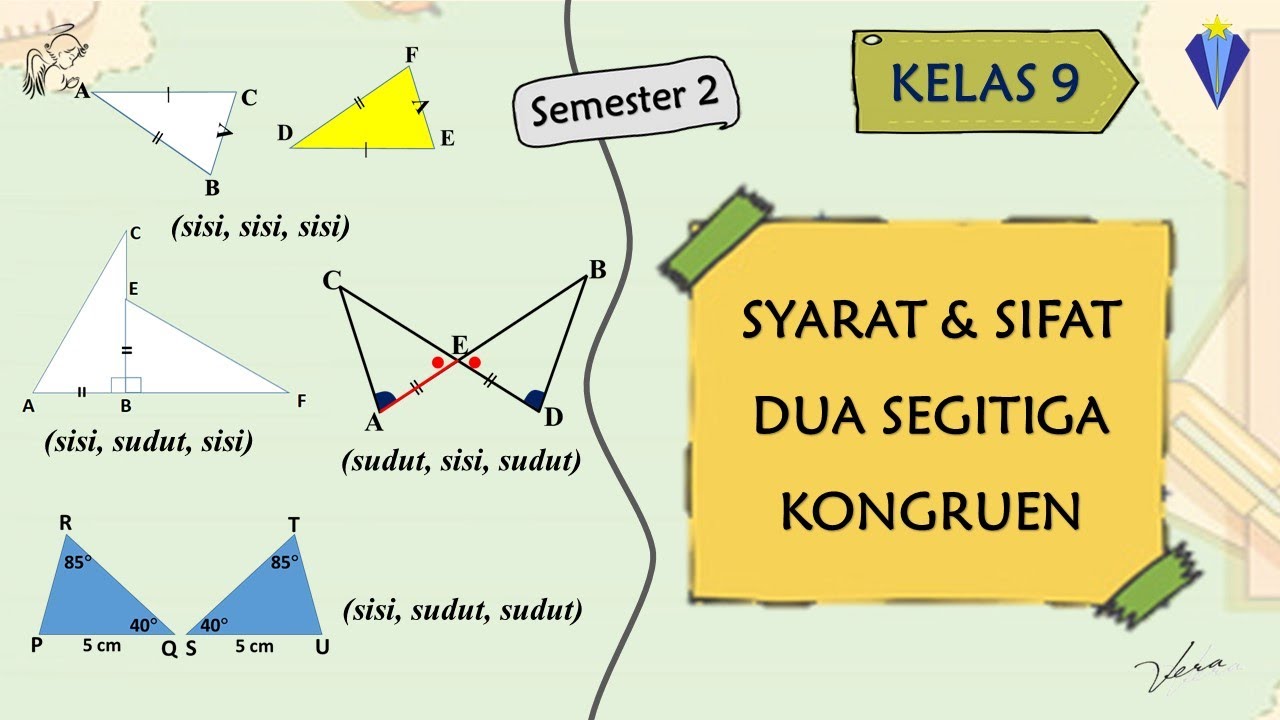
- 📏 The SSS (Side-Side-Side) criterion states that if three sides of one triangle are equal to the corresponding sides of another triangle, the triangles are congruent.
- 🔺 The SAS (Side-Angle-Side) criterion involves two sides and the included angle; if they are equal in two triangles, the triangles are congruent.
- 📐 ASA (Angle-Side-Angle) indicates that if two angles and the included side of one triangle match those of another, the triangles are congruent.
- 🌟 AAS (Angle-Angle-Side) shows that if two angles and a non-included side of one triangle are equal to those of another triangle, they are congruent.
- 🛠️ The HL (Hypotenuse-Leg) criterion applies specifically to right triangles, stating that if the hypotenuse and one leg of one right triangle are equal to those of another, they are congruent.
- 🖼️ Visual illustrations are effective in demonstrating triangle congruence and helping students understand the relationships.
- 📏 Accurate measurements of angles and sides are essential to verify triangle congruence in practical applications.
- 💡 The session encourages practice and experimentation with these principles to deepen understanding.
- 👩🏫 Students should familiarize themselves with the criteria for triangle congruence as they are fundamental in various mathematical contexts.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed is the congruence of triangles, specifically how to determine if two triangles are congruent based on their sides and angles.
What is the significance of measuring the sides and angles of triangles?
-Measuring the sides and angles of triangles is crucial for verifying their congruence, which can be established using specific criteria involving corresponding sides and angles.
What are the criteria for triangle congruence mentioned in the transcript?
-The criteria for triangle congruence mentioned include Side-Side-Side (SSS), Angle-Side-Angle (ASA), and Angle-Angle-Side (AAS) conditions.
How does the transcript suggest verifying triangle congruence?
-The transcript suggests verifying triangle congruence by measuring corresponding sides and angles using tools like rulers and protractors.
What is the consequence of having two sides and the included angle equal in two triangles?
-If two sides and the included angle of one triangle are equal to those of another triangle, the triangles are considered congruent (Angle-Side-Angle or ASA criterion).
What happens if the conditions for congruence are not met?
-If the conditions for congruence are not met, the two triangles are not considered congruent, which means they cannot be perfectly overlapped without changing their shape or size.
How does the speaker illustrate the concept of triangle congruence?
-The speaker uses examples and measurements of specific triangles to illustrate the concept of triangle congruence and walks through how to determine congruence through measuring sides and angles.
What role do labeled diagrams play in understanding triangle congruence?
-Labeled diagrams play a crucial role in understanding triangle congruence by visually representing the relationships between sides and angles, making it easier to analyze and draw conclusions.
What is the conclusion drawn about triangle congruence in the transcript?
-The conclusion drawn is that triangles can be proven congruent by meeting specific criteria, and understanding these criteria is essential for solving related problems in geometry.
What practical applications can be derived from understanding triangle congruence?
-Understanding triangle congruence has practical applications in various fields, including architecture, engineering, and design, where precise measurements and structural integrity are important.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Kekongruenan dan Kesebangunan [Part 2] - Kekongruenan Dua Segitiga

Triangle Congruence Theorems Explained: ASA, AAS, HL

Triangle Congruence Proofs Explained SSS, SAS, ASA, AAS, HL
2 SYARAT DAN SIFAT DUA SEGITIGA KONGRUEN - KESEBANGUNAN DAN KONGRUENSI - KELAS 9 SMP

Geometry Chapter 5.5 Video

KEKONGRUENAN (Materi Kelas 9 SMP)
5.0 / 5 (0 votes)
