Simplifying Radicals
Summary
TLDRIn this video, the presenter explains how to simplify radicals, focusing on the square root symbol and the importance of removing perfect square factors from under the radical. Using examples, the video demonstrates two methods for simplification: prime factorization and identifying perfect square factors. The presenter emphasizes efficiency in the process, illustrating how to break down numbers like 27 and 2800 into their factors. With practical examples and clear explanations, the video aims to equip viewers with the skills needed to simplify radicals effectively, ensuring accuracy in mathematical calculations.
Takeaways
- 😀 A radical is the square root symbol, and simplifying it involves removing perfect square factors from under the radical.
- 😀 Prime factorization is a common method used to simplify radicals by breaking down numbers into their prime components.
- 😀 For example, √27 can be simplified by factoring it into 3 and 9, leading to √27 = √9 * √3 = 3√3.
- 😀 Identifying the largest perfect square factor in a number can simplify the process, as seen in the example of √2800.
- 😀 The factors of a number are all the numbers that divide evenly into it; finding these helps in simplification.
- 😀 It’s essential to keep track of multiplication when simplifying, as mistakes can lead to incorrect results.
- 😀 A hybrid approach combining both prime factorization and perfect square identification can be effective.
- 😀 When simplifying expressions like 7√1350, first simplify the radical before multiplying by any constants outside.
- 😀 Always verify that the simplified radical maintains the same value as the original expression for accuracy.
- 😀 Simplifying radicals can become complex with larger numbers; using efficient methods can prevent errors and save time.
Q & A
What is a radical?
-A radical is a mathematical symbol that represents the square root of a number, typically denoted as √.
What does it mean to simplify a radical?
-Simplifying a radical means removing all perfect square factors from underneath the square root symbol, resulting in a simpler expression.
What is the first method introduced for simplifying radicals?
-The first method is prime factorization, where the number under the radical is broken down into its prime factors.
Can you provide an example of simplifying √27 using prime factorization?
-Yes, √27 can be simplified as √(3 × 9) = √(3 × 3 × 3) = √(3²) × √3 = 3√3.
What is the alternative method for simplifying radicals mentioned in the video?
-The alternative method involves finding the largest perfect square factor of the number under the radical and rewriting it accordingly.
How is √2800 simplified using the perfect square factor method?
-For √2800, it can be expressed as √(100 × 28) = √100 × √28 = 10√28, and further simplifying gives 20√7.
What is a hybrid approach in simplifying radicals?
-The hybrid approach combines both the prime factorization and perfect square factor methods, allowing for efficient simplification.
How does one ensure accuracy after simplifying a radical?
-To ensure accuracy, one should check that the simplified expression equals the original value by comparing decimal approximations.
What common mistake do people make when multiplying factors?
-A common mistake is confusing multiplication with addition; it's important to remember that all operations in simplification are multiplications.
Why is it important to identify perfect square factors?
-Identifying perfect square factors simplifies the process of radical simplification and helps in efficiently breaking down larger numbers.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Simplest Radical Form

LESSON 3 Simplifying Radicals (Part 2)

🦿 Langkah 027: Sifat Bentuk Akar | Fundamental Matematika Alternatifa
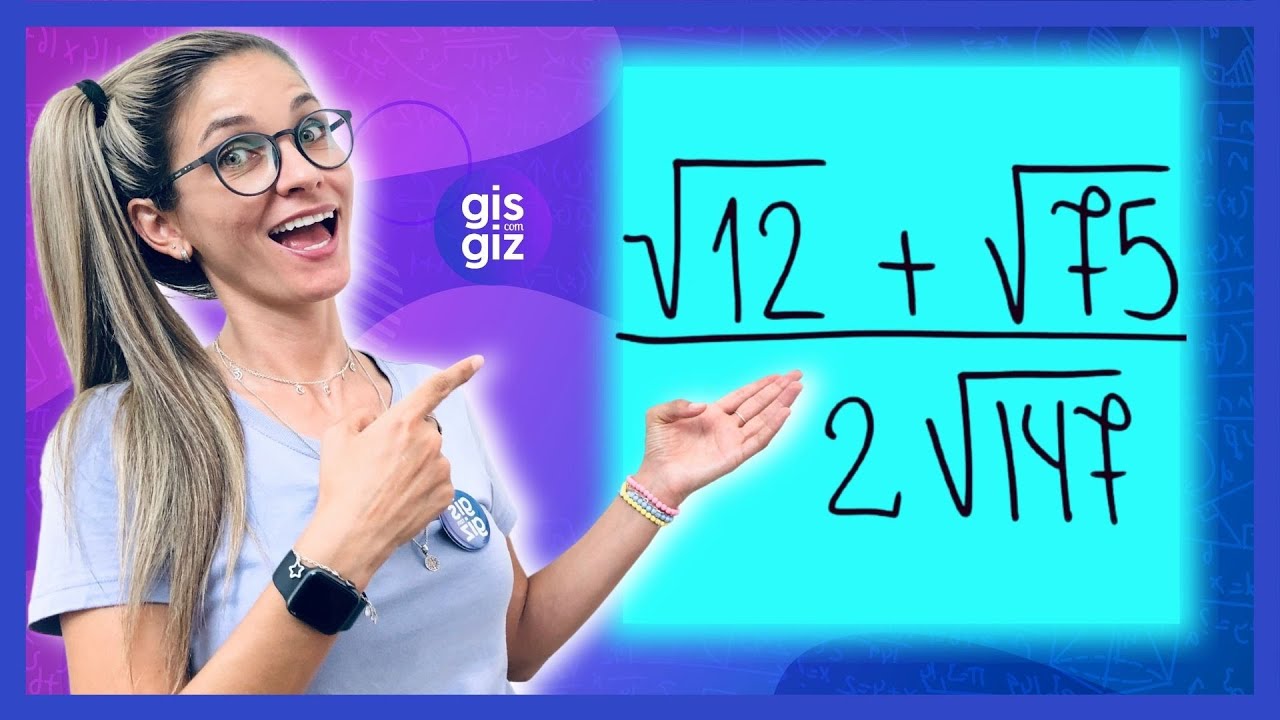
SIMPLIFICAÇÃO DE RADICAIS | SIMPLIFICAÇÃO DE RAIZ | |RADICIAÇÃO | \Prof. Gis/

SIMPLIFICACIÓN DE EXPRESIONES CON RADICALES - Ejercicio 1

SIMPLIFYING RADICAL EXPRESSIONS || GRADE 9 MATHEMATICS Q2
5.0 / 5 (0 votes)
