What Is Angular Momentum?
Summary
TLDRThis video explores the concepts of linear and angular momentum, beginning with the definition of linear momentum as the product of mass and velocity. It transitions into angular momentum, explaining its relation to rotational motion through key equations. The video derives important formulas, emphasizing the conservation of angular momentum in systems with no net torque. Real-life examples, like a spinning turntable and a figure skater's movements, illustrate how changes in inertia affect angular velocity. The engaging presentation aims to enhance understanding of these fundamental physics principles.
Takeaways
- 😀 Linear momentum is defined as the product of an object's mass and its velocity, represented by the formula p = mv.
- 🚂 A moving object, like a fast train, has significant momentum due to its mass and speed, making it hard to stop.
- 🌀 Angular momentum applies to objects that rotate around a point and is calculated using the formula L = Iω, where I is inertia and ω is angular velocity.
- 📏 The moment of inertia is the rotational equivalent of mass and varies depending on the object's shape.
- ⚙️ Angular velocity is the rotational equivalent of linear velocity, and the two are related through the equation ω = v/r.
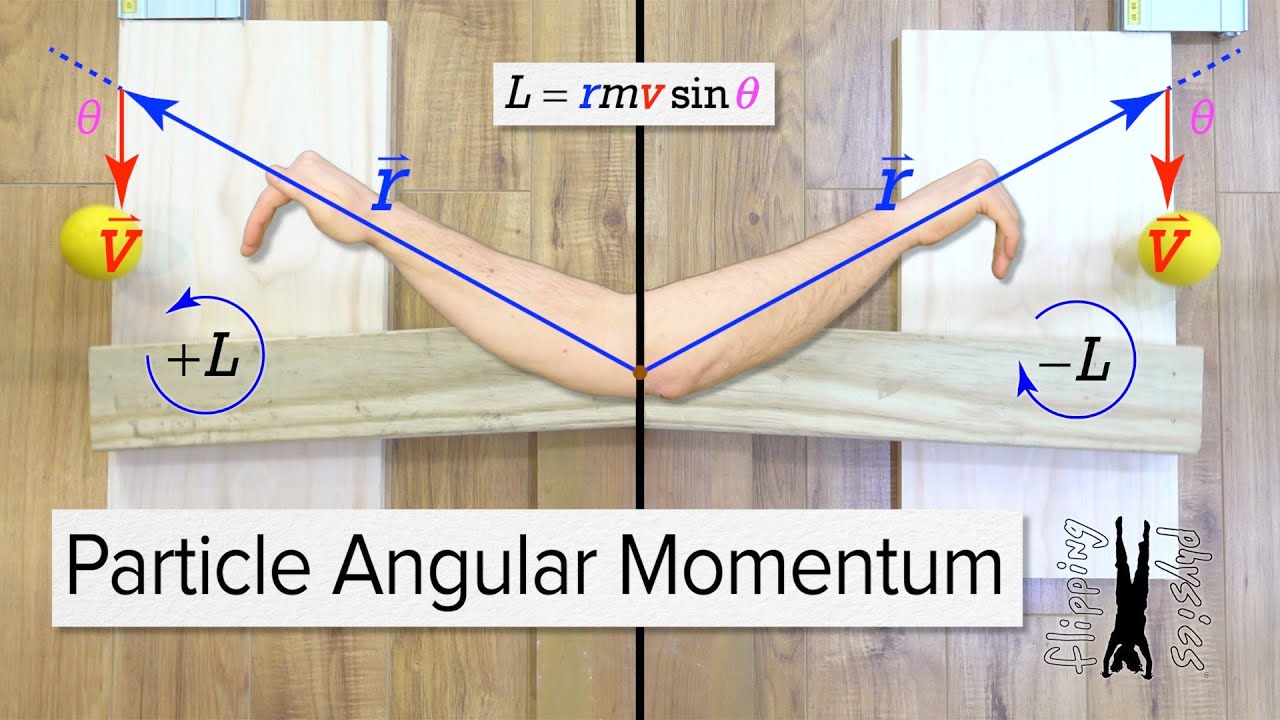
- 🔄 Angular momentum can also be expressed as L = mvr, linking it to linear momentum (p = mv) and the radius (r) of rotation.
- ⚖️ The conservation of momentum states that if no net external force acts on a system, its momentum remains constant.
- 💡 The conservation principle extends to angular momentum: if no net torque acts on a system, its angular momentum remains unchanged.
- 💪 Increasing the inertia of a rotating system will result in a decrease in angular velocity, maintaining conservation of angular momentum.
- ⛸️ A figure skater speeds up when they pull their arms in because they decrease their inertia, which leads to an increase in angular velocity.
Q & A
What is linear momentum?
-Linear momentum is the product of an object's mass and its velocity, represented by the equation p = mv, where p is momentum, m is mass, and v is velocity.
How is angular momentum defined?
-Angular momentum is defined as the product of an object's moment of inertia and its angular velocity, represented by the equation L = Iω, where L is angular momentum, I is moment of inertia, and ω is angular velocity.
Why is the symbol 'L' used for angular momentum?
-The use of 'L' to represent angular momentum is somewhat arbitrary, and the reason behind this choice is not explicitly provided in the script.
What is the relationship between linear momentum and angular momentum?
-Angular momentum can be thought of as the product of linear momentum and the radius of the circular path, expressed as L = r × p, where r is the radius and p is linear momentum.
What are the units of linear momentum?
-The units of linear momentum are kilograms times meters per second (kg·m/s), since mass is in kilograms and velocity is in meters per second.
What does the conservation of angular momentum state?
-The conservation of angular momentum states that if no net torque is acting on a system, the total angular momentum of that system remains constant.
How does adding mass to a rotating system affect its angular velocity?
-Adding mass to a rotating system increases its moment of inertia, which causes the angular velocity to decrease to conserve angular momentum, as shown by the equation L_initial = L_final.
What is the rotational equivalent of Newton's second law?
-The rotational equivalent of Newton's second law is expressed as torque = moment of inertia × angular acceleration (τ = Iα).
How does a figure skater illustrate the conservation of angular momentum?
-A figure skater demonstrates the conservation of angular momentum by pulling their arms in during a spin, decreasing their moment of inertia, which causes them to spin faster.
What is torque, and how does it relate to angular momentum?
-Torque is the rotational equivalent of force and is defined as the rate of change of angular momentum over time, represented by the equation τ = dL/dt.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)