Medidas Descriptivas Ejemplo
Summary
TLDREn este video se presentan los conceptos de medidas de tendencia central y dispersión a través de un conjunto de cinco datos. Se calculan la media aritmética, mediana y moda para entender el comportamiento central de los datos, con resultados de 41.8, 42 y 42, respectivamente. Además, se exploran medidas de dispersión, como el rango, la desviación media, la varianza y la desviación estándar, con la desviación estándar poblacional calculada en 4.83. Estos conceptos son fundamentales para analizar y comprender la variabilidad en los conjuntos de datos.
Takeaways
- 😀 La media aritmética se calcula sumando todos los datos y dividiendo entre el número total de datos.
- 😀 La mediana se obtiene ordenando los datos y tomando el valor central.
- 😀 La moda es el dato que aparece con mayor frecuencia en el conjunto.
- 😀 Las medidas de dispersión indican la variabilidad dentro de un conjunto de datos.
- 😀 El rango se calcula como la diferencia entre el valor máximo y el mínimo del conjunto de datos.
- 😀 La desviación media se obtiene sumando las diferencias absolutas de cada dato respecto a la media y dividiendo por el número de datos.
- 😀 La varianza se calcula sumando las diferencias cuadráticas respecto a la media y dividiendo por el número de datos.
- 😀 Para calcular la desviación estándar poblacional, se toma la raíz cuadrada de la varianza.
- 😀 En este conjunto, la media aritmética es 41.8, la mediana es 42, y la moda también es 42.
- 😀 La desviación estándar poblacional del conjunto de datos es aproximadamente 4.83.
Q & A
¿Qué es la media aritmética y cómo se calcula?
-La media aritmética, o promedio, se obtiene sumando todos los datos y dividiendo el resultado entre el número total de datos. En este caso, se suman 35, 40, 42, 42 y 50, resultando en 41.8.
¿Cuál es la mediana de este conjunto de datos?
-La mediana es 42. Se obtiene ordenando los datos de menor a mayor y tomando el valor que se encuentra en la posición central.
¿Qué representa la moda en un conjunto de datos?
-La moda es el dato que aparece con mayor frecuencia. En este caso, el 42 es la moda, ya que tiene una frecuencia de aparición de 2.
¿Qué son las medidas de dispersión y por qué son importantes?
-Las medidas de dispersión indican la uniformidad de un conjunto de datos. Son importantes porque nos ayudan a entender cómo varían los datos alrededor de la media.
¿Cómo se calcula el rango de un conjunto de datos?
-El rango se calcula restando el valor más pequeño del valor más grande del conjunto. Es siempre un valor positivo.
¿Qué es la desviación media y cómo se calcula?
-La desviación media se obtiene sumando las diferencias absolutas entre cada dato y la media aritmética, y dividiendo el resultado entre el número de datos. En este caso, es 3.44.
¿Qué es la varianza y cómo se calcula en este contexto?
-La varianza mide la dispersión cuadrática de los datos respecto de la media aritmética. Se calcula sumando las diferencias cuadráticas de cada dato respecto a la media y dividiendo entre el número total de datos.
¿Cuál es la diferencia entre la desviación media y la varianza?
-La desviación media es la media de las diferencias absolutas respecto a la media, mientras que la varianza es la media de las diferencias cuadráticas respecto a la media.
¿Cómo se obtiene la desviación estándar poblacional?
-La desviación estándar poblacional se obtiene calculando la raíz cuadrada de la varianza. En este caso, es 4.83.
¿Por qué es relevante conocer la desviación estándar en un conjunto de datos?
-La desviación estándar es relevante porque proporciona información sobre la variabilidad de los datos. Un valor más alto indica mayor dispersión, mientras que un valor más bajo indica que los datos están más concentrados alrededor de la media.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Medidas de Dispersión o Variabilidad - Introducción

MEDIA, MODA Y MEDIANA Super facil | Medidas de tendencia central

Estadística Descriptiva: Medidas de Síntesis (I). Módulo 2

MEDIA, MODA y MEDIANA Muy Fácil - Medidas de Tendencia Central
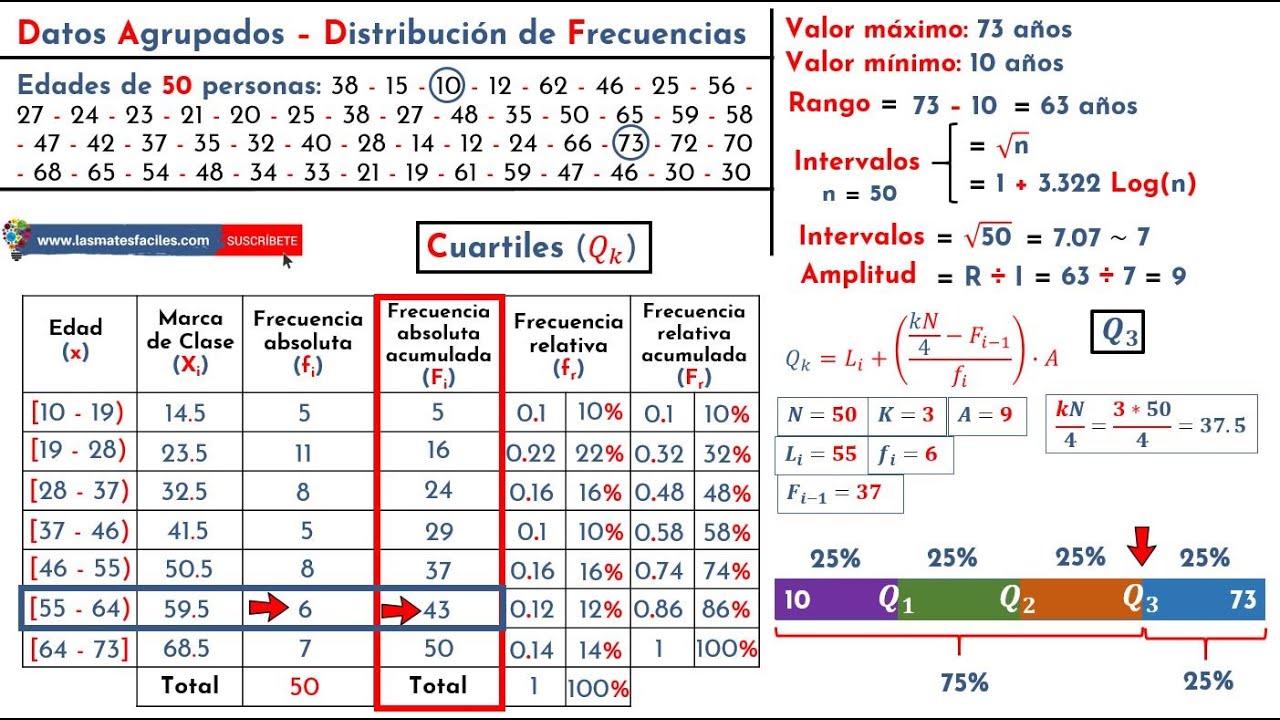
Cuartiles, Deciles y Percentiles - Datos Agrupados

10. Estimación puntual e intervalos de confianza | DATOS 2.0 MINI
5.0 / 5 (0 votes)
