CONTINUIDAD de una FUNCIÓN a partir de la GRÁFICA 📈 Ejercicios resueltos 💙
Summary
TLDREn este video, el presentador enseña cómo analizar la continuidad de una función matemática, explicando de manera clara cuándo una función es continua o discontinua. Utiliza gráficos y ejemplos para ilustrar puntos clave, como identificar saltos en las funciones y cómo describirlas correctamente en términos de x. Además, proporciona recomendaciones musicales para acompañar el estudio de matemáticas y reta a los espectadores a analizar la continuidad de otra función. El tono es dinámico y accesible, invitando a los usuarios a aprender de forma entretenida y práctica.
Takeaways
- 📏 La continuidad de una función se refiere a si se puede trazar sin levantar el lápiz del papel.
- ⚠️ Cuando hay un salto en la gráfica de una función, eso indica una discontinuidad.
- 🖊️ Para analizar la continuidad, se debe identificar si se puede trazar la gráfica completamente o si hay interrupciones.
- 🔢 La discontinuidad ocurre en puntos específicos, como en el ejemplo de la función con x igual a -2.
- ✍️ Si la función es continua, se puede describir como continua en R, lo que significa que no hay saltos en ningún valor de x.
- 🧮 Otra forma de expresar continuidad es decir que la función es continua de menos infinito a infinito.
- 🌊 Las discontinuidades pueden abarcar intervalos completos, no solo puntos individuales.
- 📝 En el caso de discontinuidades, se deben nombrar los puntos inicial y final del intervalo discontínuo, como en el intervalo de x = 2 a x = 4.
- 🎶 El video ofrece una sugerencia musical para acompañar el estudio: una canción llamada 'Just Take You Love' de Fort Ay Love.
- 🧐 Se deja una función como ejercicio para que los espectadores analicen la continuidad por sí mismos.
Q & A
¿Qué tema trata la clase de matemáticas en el guion?
-La clase trata sobre la propiedad de continuidad de las funciones.
¿Qué es la continuidad de una función según el guion?
-La continuidad es la propiedad que indica si se puede trazar la función de golpe sin levantar el lápiz del papel en ningún momento.
¿Cómo se identifica una discontinuidad en una función?
-Una discontinuidad se identifica cuando hay un salto en la gráfica de la función, es decir, un punto donde no se puede trazar la función sin levantar el lápiz.
¿Cuál es el procedimiento para analizar la continuidad de una función?
-Primero se identifica el punto de la discontinuidad y luego se determina el valor de x en ese punto.
¿Cómo se indica que una función es continua en todos los números reales?
-Se escribe que la función es continua en R o de -infinito a infinito.
¿Qué significa que una función no sea continua en un punto específico?
-Significa que en ese punto hay una discontinuidad, un salto en la gráfica de la función.
¿Cómo se indica que una función es continua en un intervalo específico?
-Se escribe que la función es continua en el intervalo de izquierda a derecha, nombrando los valores de x inicial y final del intervalo.
¿Qué es el 'tip del día' que se menciona en el guion?
-El 'tip del día' es un consejo para analizar la continuidad de una función, que sugiere localizar el punto de la discontinuidad y luego encontrar el valor de x en ese punto.
¿Cuál es la recomendación musical del día según el guion?
-La recomendación musical del día es el tema 'Just Take You Love' del grupo Fort Ay Love.
¿Qué se nos invita a hacer con la canción mencionada al final del guion?
-Se nos invita a disfrutar de la canción mientras se trabaja en matemáticas.
¿Cuál es el ejercicio propuesto al final del guion?
-El ejercicio propuesto es analizar la continuidad de una función adicional y dejar un comentario sobre la continuidad que se percibe.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Continuidad de una función | Ejemplo 3

►¿Cómo Calcular Límites y Continuidades de la Gráfica de una Función?

[SER222] Asymptotics (2/5): Upper Bounds

Explicación del Teorema de Bolzano
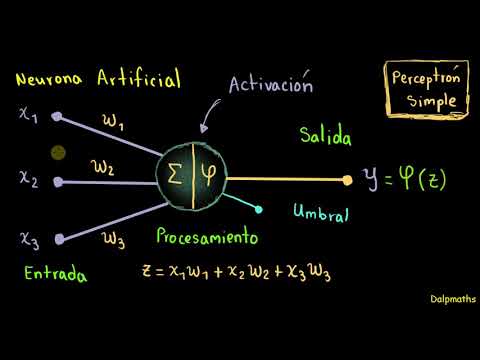
Redes neuronales: Introducción al perceptrón simple.

¿Cómo saber si es función o no? Criterio Línea vertical | Curso de relaciones y funciones
5.0 / 5 (0 votes)
