08-3) Integral de área HB

Summary

En la clase pasada, se abordó el cálculo del área bajo la curva de la función 1/x utilizando la técnica de subdivisión y aproximación mediante rectángulos. En esta clase, se extiende el concepto para calcular el área definida para un polinomio, demostrando cómo se puede aproximar el área mediante la sumatoria de áreas de rectángulos y trapecios. Se resalta la importancia de la programación y las matemáticas para resolver problemas de integrales, y se sugiere el uso de herramientas como Wolfram Alpha para validar los resultados. Además, se anima a los estudiantes a practicar y comprender profundamente los temas para tener éxito en las aplicaciones futuras.

Takeaways

• 📚 La clase pasada se habló del cálculo del logaritmo natural y se introdujo el concepto de integral como el área bajo la curva de una función.
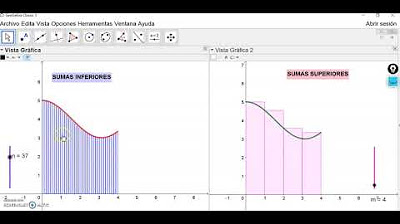
• 📈 El área bajo la curva de una función puede ser aproximada mediante subdivisiones, utilizando rectángulos para calcular el área.
• 🤔 Se exploró cómo el error en la aproximación disminuye a medida que se incrementa el número de subdivisiones, haciéndolos más delgados.
• 📊 Se comparó el área calculada mediante la suma de rectángulos con el valor matemático ideal de la integral, mostrando la aproximación al valor correcto.
• 👨‍🏫 Se presentó un ejemplo práctico de cómo calcular el área bajo la curva de un polinomio, utilizando la técnica de subdivisión.
• 🔢 Se modificó el programa de la clase anterior para adaptarlo al cálculo de la integral de un polinomio en lugar del logaritmo natural.
• 💻 Se enfatizó la importancia de la programación y cómo se puede utilizar para resolver problemas matemáticos complejos.
• 📈 Se introdujo el concepto de 'trapecios' como una mejora en la aproximación del área, reduciendo el error en comparación con los rectángulos.
• 🔍 Se utilizó WolframAlpha como una herramienta para verificar los resultados de los cálculos y para resolver integrales matemáticas.
• 🎯 Se destacó la importancia de la práctica y la comprensión de las matemáticas para comprender y aplicar correctamente los conceptos vistos en clase.
• 🚀 Se animó a los estudiantes a enfocarse en la asignatura y a practicar los conceptos aprendidos para tener éxito en las clases futuras.

Q & A

¿Qué se discutió en la clase anterior?

En la clase anterior se discutió sobre el logaritmo natural y se trabajó en encontrar el área bajo la curva de la función 1/x, utilizando la técnica de subdivisión con rectángulos para aproximar el cálculo integral.

¿Qué es la integral y qué representa?

La integral representa el área bajo la curva de una función. Es un concepto fundamental en el cálculo para calcular áreas, volumes y otros valores relacionados con la distribución de funciones matemáticas.

¿Cómo se aproximó el cálculo de la integral en la clase?

Se aproximó el cálculo de la integral dividiendo el segmento de integración en n partes iguales y sumando las áreas de los rectángulos formados, cada uno con base delta x y altura igual a la evaluación de la función en ese punto.

¿Qué es delta x y cómo se utiliza en el proceso de integración?

Delta x es la anchura de los rectángulos utilizados en la aproximación de la integral. Se utiliza para dividir el intervalo de integración en partes iguales y calcular el área de cada rectángulo, que luego se suma para obtener la aproximación del área total bajo la curva.

¿Qué se hizo en la clase para mejorar la aproximación de la integral?

Para mejorar la aproximación, se incrementó el número de subdivisiones, es decir, se hizo delta x más pequeño, lo que hizo que los rectángulos fueran más delgados y la sumatoria de sus áreas se acercara más al área bajo la curva real.

¿Cómo se puede calcular el área bajo la curva de un polinomio?

Se puede calcular el área bajo la curva de un polinomio aplicando el mismo proceso que se utilizó para la función 1/x, pero en este caso, evaluando el polinomio en cada punto y sumando las áreas de los rectángulos o trapecios formados por subdividir el intervalo de integración.

¿Qué es WolframAlpha y cómo se puede utilizar para resolver integrales?

WolframAlpha es un motor de búsqueda y un sistema de inteligencia artificial en línea que se puede utilizar para resolver cálculos matemáticos complejos, incluyendo integrales. Se puede ingresar la función y los límites de integración en WolframAlpha y el sistema proporcionará el valor de la integral y, a menudo, una gráfica de la función.

¿Cómo se puede mejorar la precisión del cálculo de la integral utilizando trapecios en lugar de rectángulos?

Al utilizar trapecios en lugar de rectángulos, se tiene en cuenta la curvatura de la función y se reduce el error de aproximación. El área de cada trapezium es calculada como la mitad de la suma de las alturas de los dos puntos que forman el trapezium, lo que resulta en una aproximación más precisa del área bajo la curva.

¿Qué se pidió a los estudiantes como actividad para la siguiente clase?

Se pidió a los estudiantes que desarrollen el código de programación para calcular el área bajo la curva de un polinomio utilizando la técnica de los trapecios, basándose en el conocimiento adquirido en la clase.

¿Qué se enfatizó como parte importante para la comprensión de las siguientes clases?

Se enfatizó que es importante tener una sólida comprensión de las matemáticas y los conceptos relacionados con los integrales para poder comprender y aplicar correctamente los temas que se van a discutir en las siguientes clases, que incluyen aplicaciones en tercera dimensión.