ILLUSTRATING LINEAR INEQUALITIES IN TWO VARIABLES || GRADE 8 MATHEMATICS Q2
Summary
TLDRThis video tutorial focuses on linear inequalities in two variables, contrasting them with linear equations by highlighting the absence of equal signs and presence of relational symbols like 'greater than' and 'less than'. It explains how to identify and solve linear inequalities, using examples to demonstrate how ordered pairs can be solutions if they satisfy the inequality. The video also covers the graphical representation of linear inequalities, showing how they form half-planes on a graph, and concludes with exercises for viewers to test their understanding.
Takeaways
- 🔢 Linear inequalities in two variables are mathematical statements involving two variables and inequality symbols such as <, >, ≤, or ≥.
- 📐 The key difference between linear equations and linear inequalities is that equations use the equal sign (=), while inequalities use <, >, ≤, or ≥.
- 📋 A linear inequality in two variables can be expressed in four forms: ax + by > c, ax + by < c, ax + by ≥ c, or ax + by ≤ c, where a, b, and c are real numbers and a and b are not zero.
- 📈 An ordered pair (x, y) is a solution to a linear inequality if substituting the values of x and y into the inequality results in a true statement.
- 📉 The graph of a linear inequality in two variables is a half-plane, which is a region of the coordinate plane that satisfies the inequality.
- 📌 Linear inequalities are represented on a graph with a solid or dashed line to indicate the boundary, with the half-plane containing the solutions shaded.
- 👉 When determining if an ordered pair is a solution to a linear inequality, substitute the x and y values from the pair into the inequality and check if the resulting statement is true.
- ❌ The script clarifies that not all ordered pairs will satisfy a given inequality, and only those that make the inequality true are considered solutions.
- 📖 The video tutorial provides examples of how to determine if ordered pairs are solutions to specific linear inequalities, such as 4x + 5y > 20.
- 🎓 The script is part of a series of educational videos aimed at teaching math lessons, specifically focusing on linear inequalities in two variables.
Q & A
What is the main topic of the video?
-The main topic of the video is illustrating linear inequalities in two variables, differentiating them from linear equations, and determining whether an ordered pair is a solution to a given linear inequality.
What are the objectives of the video?
-The objectives are to illustrate linear inequalities in two variables, differentiate them from linear equations in two variables, and determine if an ordered pair is a solution to a given linear inequality.
How does the video introduce the concept of linear inequalities?
-The video introduces linear inequalities by having viewers group mathematical statements into linear equations and linear inequalities, highlighting the use of inequality symbols like less than, greater than, less than or equal to, and greater than or equal to.
What is the difference between a linear equation and a linear inequality?
-A linear equation uses an equal sign, while a linear inequality uses symbols like less than, greater than, less than or equal to, or greater than.
What are the four forms of linear inequalities in two variables?
-The four forms are: 1) ax + by > c, 2) ax + by < c, 3) ax + by ≥ c, and 4) ax + by ≤ c, where a, b, and c are real numbers and a and b are not equal to zero.
How is an ordered pair considered a solution to a linear inequality?
-An ordered pair (x, y) is a solution to a linear inequality if substituting the values of x and y into the inequality results in a true statement.
Can you provide an example from the video of determining if an ordered pair is a solution to a linear inequality?
-Yes, the video provides an example with the inequality 4x + 5y > 20. For the ordered pair (2, 5), substituting x=2 and y=5 results in 4*2 + 5*5 = 33, which is greater than 20, so (2, 5) is a solution.
How does the video explain the graphical representation of a linear inequality?
-The video explains that the graph of a linear inequality is a half-plane, consisting of all points that satisfy the inequality, and it can be represented by a broken or solid line.
What is the significance of the terms 'solution' and 'not a solution' in the context of linear inequalities?
-In the context of linear inequalities, 'solution' refers to ordered pairs that satisfy the inequality, making the statement true, while 'not a solution' refers to ordered pairs that do not satisfy the inequality, resulting in a false statement.
How does the video conclude the tutorial on linear inequalities?
-The video concludes by encouraging viewers to practice determining whether given ordered pairs are solutions to linear inequalities and reminding them to like, subscribe, and hit the notification bell for more tutorials.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

cara cepat sistem pertidaksamaan linier dua variabel dari grafik
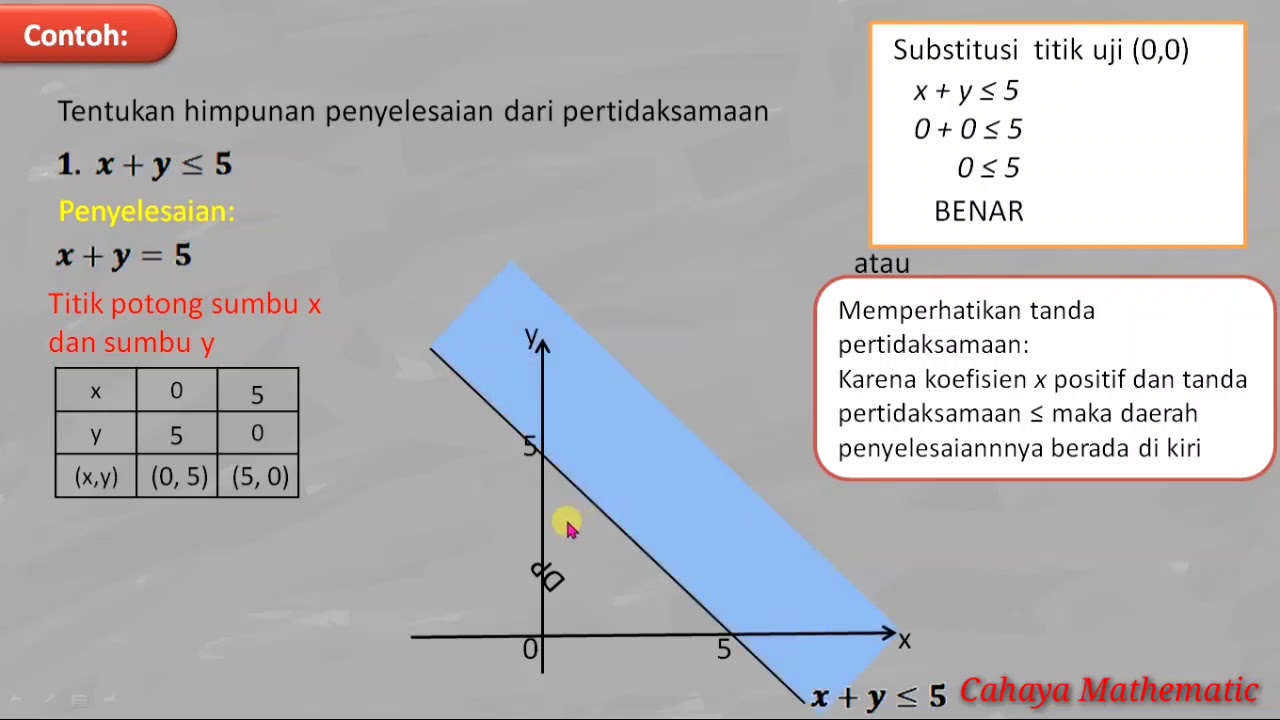
PERTIDAKSAMAAN LINEAR DUA VARIABEL
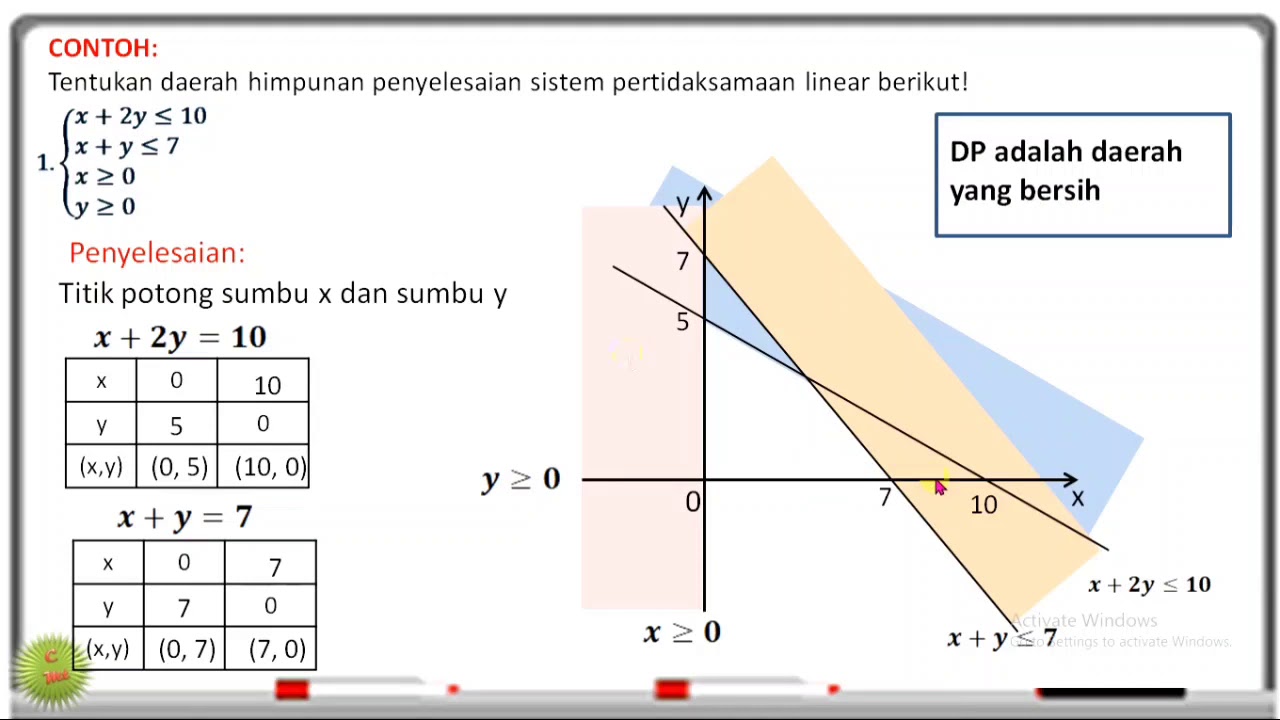
SISTEM PERTIDAKSAMAAN LINEAR DUA VARIABEL SPtLDV

8TH EDITION | BOOK 2 | EXERCISE 3A | QUESTION # 1, 2, 3

Translating Words To Algebraic Expressions Explained!
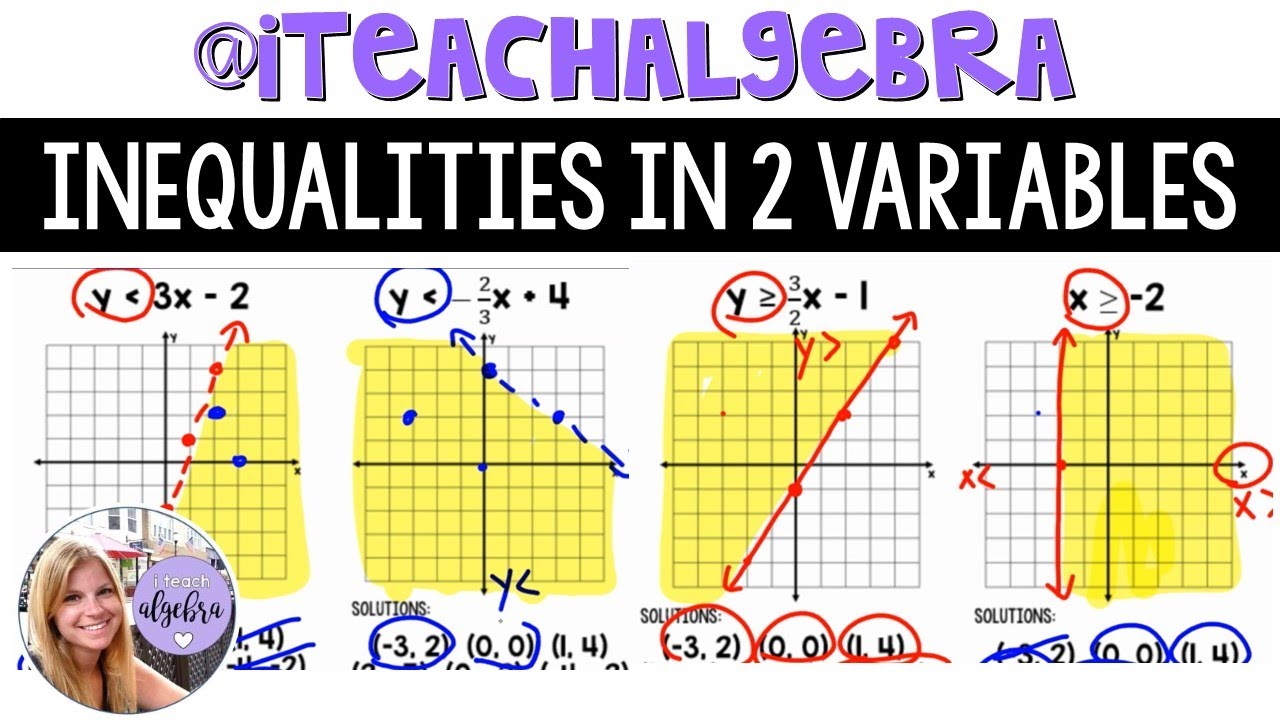
Algebra 1 - Graphing Inequalities in Two Variables
5.0 / 5 (0 votes)
