Metodo de Newton-Raphson | Explicación y ejercicio resuelto
Summary
TLDRThis video from the Physics and Math channel offers a detailed and easy-to-understand explanation of Newton-Raphson method, a powerful technique for finding roots of equations. The host walks viewers through the method's definition, its iterative nature, and its geometric interpretation. A step-by-step demonstration is provided, starting with an initial guess close to the root, followed by successive approximations using the derivative of the function. The video includes a practical example, where the method is applied to find an approximate root of a given function, showcasing how quickly the approximations converge to the actual root. The host emphasizes the importance of accurate calculations with each iteration to achieve a precise result.
Takeaways
- 📚 The video is an educational tutorial explaining the Newton-Raphson method in detail, a technique used to find the roots of equations.
- 🔍 The main objective of the Newton-Raphson method is to estimate the solution of an equation \( F(x) = 0 \) by producing a sequence of approximations that get closer to the solution.
- 📈 The method involves selecting an initial guess \( x_0 \) close to the root and then iteratively refining this guess using the method's formula.
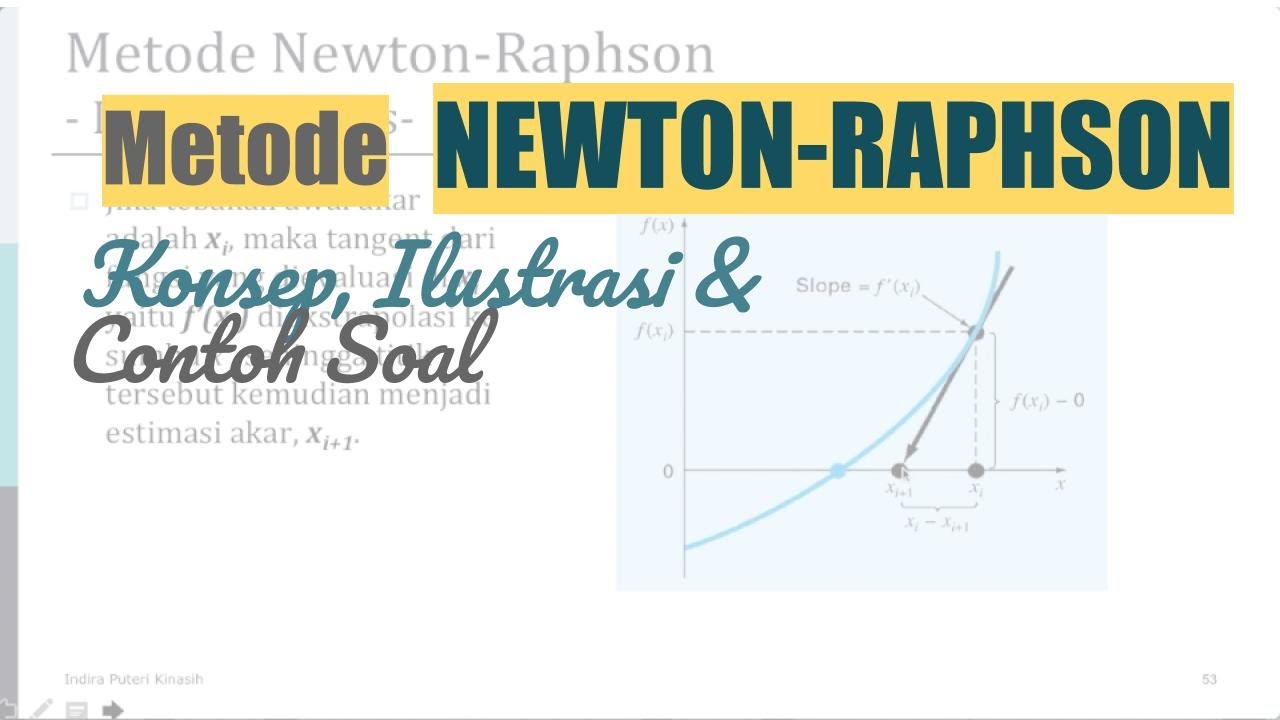
- 📝 A geometric explanation of the method is provided, where the tangent line to the function at a point is used to find the next approximation.
- 📉 The iterative process is demonstrated graphically, showing how starting from \( x_0 \), the method quickly converges to the root with just a few iterations.
- 👨🏫 The tutorial includes a step-by-step guide on how to apply the Newton-Raphson method, starting with an initial guess and using the formula to find subsequent approximations.
- 📚 An analytical explanation is given on how to use the method with numbers, emphasizing the importance of using the first approximation to find the second, and so on.
- 🔢 The video includes a practical example problem where the method is applied to find an approximation of a root for a given function, starting with \( x = 1 \).
- 📉 A graphical representation of the function and its root is provided to help viewers understand the starting point and the iterative process visually.
- 🔄 The iterative formula used in the Newton-Raphson method is explained and demonstrated through the calculation of successive approximations.
- 📝 The difficulty of the method is highlighted, noting that it requires careful substitution of values into the function and its derivative for accurate results.
Q & A
What is the objective of the Newton-Raphson method?
-The objective of the Newton-Raphson method is to estimate the solution of an equation F(x) = 0 by finding the roots of the equation through successive approximations.
How do we start the Newton-Raphson method?
-We start the Newton-Raphson method by choosing an initial guess x₀, which is a number close to the root.
What are the iterations in the Newton-Raphson method?
-Iterations in the Newton-Raphson method are successive approximations that move closer to the root with each step.
What is the geometric explanation of the Newton-Raphson method?
-Geometrically, the method involves drawing a tangent line at the initial point and finding its intersection with the x-axis. This process is repeated with each new point until the approximation is close enough to the actual root.
How do we perform the first iteration in the Newton-Raphson method?
-The first iteration is performed by taking the initial guess x₀, calculating the tangent at this point, and finding the intersection with the x-axis to get the next approximation x₁.
What is the formula used in the Newton-Raphson method?
-The formula used is xₙ₊₁ = xₙ - f(xₙ) / f'(xₙ), where xₙ is the current approximation, f(xₙ) is the function value at xₙ, and f'(xₙ) is the derivative value at xₙ.
What is the significance of the derivative in the Newton-Raphson method?
-The derivative helps determine the slope of the tangent line at each approximation point, which is crucial for calculating the next approximation.
How do we know when to stop iterating in the Newton-Raphson method?
-We stop iterating when the successive approximations are sufficiently close to the actual root, usually determined by a predefined tolerance level.
What example function is used in the video to illustrate the Newton-Raphson method?
-The example function used is x³ - x - 1 = 0.
What initial guess is used in the video example, and what root does it approximate?
-The initial guess used in the video example is x₀ = 1, and it approximates the root to be around 1.32 after several iterations.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
Metode Newton Raphson (Konsep & Contoh) [Metode Numerik]

METODE NUMERIK P7 PART 1/2 | METODE NEWTON-RAPHSON UNTUK MENYELESAIKAN PERSAMAAN NON LINIER

Newton Raphson Load Flow Solution - 3 Bus - Part 1 of 3

priv

8. METODE LELARAN TITIK TETAP - FIX POINT ITERATION - METODE NUMERIK
SPLDV (Sistem persamaan linear dua variabel) Metode grafik
5.0 / 5 (0 votes)
