Media o valor esperado, varianza y desviación estándar de variable aleatoria discreta
Summary
TLDREn este video, el profesor Jorge de Mate Móvil enseña cómo calcular la media, la varianza y la desviación estándar de una variable aleatoria discreta. A través de un ejemplo práctico con una tabla de probabilidades, se explica paso a paso cómo aplicar las fórmulas correspondientes. Jorge enfatiza la utilidad de la tabla para organizar los cálculos y evitar errores, destacando que la desviación estándar se calcula simplemente tomando la raíz cuadrada de la varianza. El video ofrece una guía clara y accesible para estudiantes que buscan dominar estos conceptos fundamentales en estadística.
Takeaways
- 😀 La media o valor esperado de una variable aleatoria discreta se calcula multiplicando cada valor de la variable por su probabilidad y sumando los productos obtenidos.
- 😀 La media es un promedio ponderado, lo que significa que los valores de la variable aleatoria son ponderados según sus probabilidades.
- 😀 Es importante verificar que la suma de las probabilidades en la tabla sea igual a 1 para asegurar que la distribución sea válida.
- 😀 La varianza mide la dispersión de una variable aleatoria respecto a su media, y se calcula usando una fórmula que involucra la suma de los productos de los valores al cuadrado y sus probabilidades.
- 😀 Para calcular la varianza, se puede usar la fórmula rápida: sumar los productos de los valores al cuadrado por sus probabilidades y restar la media al cuadrado.
- 😀 La desviación estándar es simplemente la raíz cuadrada de la varianza, proporcionando una medida de dispersión más intuitiva.
- 😀 Al calcular la media, varianza y desviación estándar, se recomienda utilizar la tabla de distribución de probabilidad para mantener los cálculos organizados y evitar errores.
- 😀 Es posible calcular estos parámetros sin usar la tabla, pero usarla facilita el proceso y asegura que los cálculos estén bien ordenados.
- 😀 En el caso de la desviación estándar, se toma el valor de la varianza y se le aplica la raíz cuadrada para obtener el resultado final.
- 😀 Aunque se puede usar la fórmula larga para calcular la media, varianza y desviación estándar, la tabla es la forma más eficiente y ordenada de hacerlo, especialmente para cálculos rápidos y múltiples.
Q & A
¿Qué se va a calcular en el video?
-En el video se va a calcular la media o valor esperado, la varianza y la desviación estándar de una variable aleatoria discreta.
¿Qué es la media o valor esperado de una variable aleatoria discreta?
-La media o valor esperado es un promedio ponderado de los valores de la variable aleatoria, donde los pesos son las probabilidades asociadas a cada valor.
¿Cómo se calcula la media o valor esperado según el video?
-La media o valor esperado se calcula sumando los productos de cada valor de la variable aleatoria y su respectiva probabilidad.
¿Qué fórmula se usa para calcular la varianza?
-La varianza se calcula usando la fórmula: varianza = sumatoria de (x^2 * fx) - (media)^2, donde x es el valor de la variable aleatoria y fx es la probabilidad asociada.
¿Por qué se utiliza una tabla para calcular la media, varianza y desviación estándar?
-Se utiliza la tabla porque organiza los cálculos de manera ordenada, lo que facilita detectar errores rápidamente y hace que los cálculos sean más simples y claros.
¿Cuál es la importancia de la probabilidad total en la distribución de una variable aleatoria?
-La probabilidad total debe ser igual a 1, lo que garantiza que todas las probabilidades asignadas a los valores posibles de la variable aleatoria estén distribuidas correctamente.
¿Cómo se calcula la desviación estándar de una variable aleatoria discreta?
-La desviación estándar se calcula tomando la raíz cuadrada positiva de la varianza.
¿Por qué es importante usar las fórmulas adecuadas para la varianza y la desviación estándar?
-Es importante usar las fórmulas adecuadas porque permiten calcular de manera más eficiente y rápida los valores correctos, evitando errores comunes al usar fórmulas más complejas.
¿Qué significa que la media, la varianza y la desviación estándar sean medidas de tendencia central y dispersión?
-La media es una medida de tendencia central que describe el valor promedio de los datos, mientras que la varianza y la desviación estándar son medidas de dispersión que muestran cuán dispersos están los valores respecto a la media.
¿Se puede usar la fórmula tradicional para calcular la media en lugar de la tabla?
-Sí, se puede usar la fórmula tradicional multiplicando cada valor de la variable por su probabilidad y sumando los resultados, pero la tabla es más práctica y eficiente para calcular la media, varianza y desviación estándar.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Rango, varianza, desviación estándar, coeficiente de variación, desviación media: datos no agrupados

Varianza y Desviación Estándar de Datos Agrupados de Variable Discreta

Varianza y Desviación Estándar - Fórmulas Rápidas

Función de probabilidad de variable aleatoria discreta | Ejercicio 1

Varianza y Desviación Estándar - Ejercicio 2
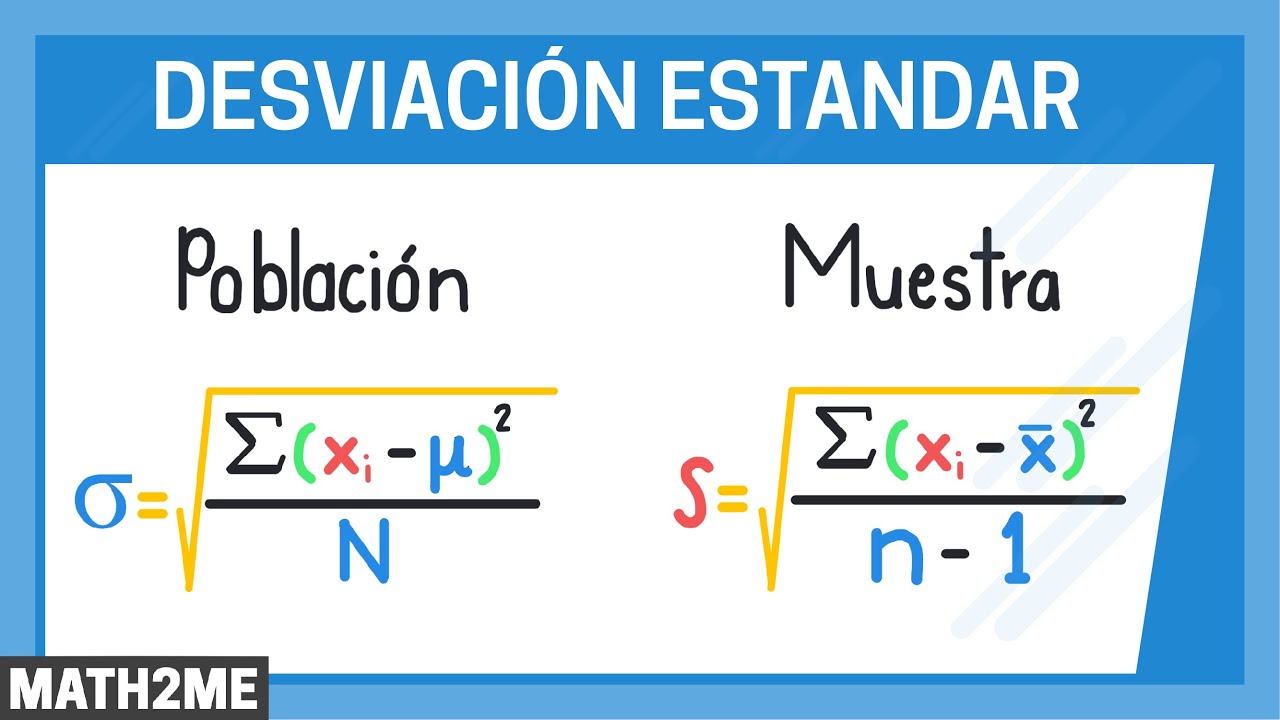
Desviación estándar en una población y muestra | Introdución | Fx-991EX
5.0 / 5 (0 votes)
